При каких значениях параметры

Данное неравенство верно для всех х, если коэффициент при x² отрицательный и дискриминант квадратного уравнения (p-5)x²+(2p-4)x-p-3=0 - отрицательный, т.е. имеем систему неравенств

Решением второго неравенства есть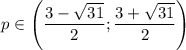

ответ: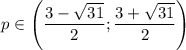

Объяснение:

Проверим случай p=5, уйдет квадратичная часть, но линейная останется, значит неравенство не будет выполняться для всех x.

При p не равном 5 график левой части неравенства представляет собой параболу, для того, чтобы неравенство было верно для любого x вся парабола должна лежать ниже оси абсцисс, т. е. ветви вниз(p-5<0) и D(дискриминант)<0.

D1=(2p-4)^2-4(p-5)(-p-3)=8p^2-24p-44<0

2p^2-6p-11<0

D2=36+88=124

p1=(3-sqrt(31))/2

p2=(3+sqrt(31))/2

D1<0 при

Эти значения p меньше пяти(т.е. ветви направлены вниз). Заносим их в ответ.