При каких значениях параметра а уравнение имеет один корень 16^x-(a+1)*4^x+a=0

Ответы

kodraemail 07.06.2020 00:12

$\displaystyle 16^x-(a+1)\cdot4^x+a=0\\\\4^{2x}-4^x(a+1)+a=0\\\\4^x=t,\quad t0\\\\t^2-t(a+1)+a=0\\\\D=(a+1)^2-4a=a^2-2a+1=(a-1)^2$

Рассмотрим два случая

1) Дискриминант равен 0

2) Дискриминант больше 0

Рассматривать случай при дискриминанте меньше 0 смысла нет, так как никаких действительных корней в этом случае не будет.

$\displaystyle 1)\quad \text{D}=0\quad\rightarrow\quad(a-1)^2=0\quad \rightarrow \quad \boxed{a=1}\\\\t=\frac{a+1}{2}=\frac{1+1}2=1\quad (t0)\\\\2)\quad \text{D}0\quad\rightarrow\quad(a-1)^20\quad \rightarrow\quad a\in(-\infty;1)\cup(1;+\infty)\\\\t=\frac{-b\pm\sqrt{D}}{2a}\\\\t_1=\frac{a+1-(a-1)}{2}=\frac{2}2=1\\\\t_2=\frac{a+1+a-1}{2}=\frac{2a}2=a$

Первый корень всегда: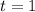 t=1

Второй корень может принимать как положительные, так и отрицательные значения: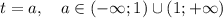 $t=a,\quad a\in(-\infty;1)\cup(1;+\infty)$

При этом, вспомним про условие: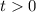

Показательная функция принимает строго положительные значения. Значит, если а будет меньше или равно 0, то второго корня у исходного уравнения не будет.

$\displaystyle \left \{ {{a\in(-\infty;1)\cup(1;+\infty)} \atop {a\leq0}} \right. \quad\rightarrow\quad \boxed{a\in(-\infty;0]}$