При каких значениях параметра а уравнение ax= (модуль x ) + (модуль x -1) имеет ровно 2 решения?

х=0 - не может быть решением данного уравнения, так как

a*0=0

|0|+|0-1|=0+1=1

0 не равно 1

перепишем данное уравнение в виде

Построим график правой части

при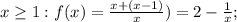

y=a - эта пряммая параллельная оси Ох,

из графика видно, что при a>=2 одно решение (одна точка пересечения)

при 1<a<2 - два решения (две точки пересечения)

при a=1 - одно решение

при -2<=a<1 - нет решений

при a<-2 - одно решение

ответ: при 1<a<2