При каких значениях параметра а существует единственная пара чисел (х; у) удовлетворяющая системе

Ответы

hromovaysoydwfz 26.07.2020 21:58

Рассмотрим неравенство:

$3x^2+3xy+2y^2=3x^2+3xy+0.75y^2+1.25y^2=(\sqrt{3}x+\frac{\sqrt{3}}{2}y)^2+1.25y^2\geq 0$

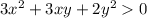1. Если 3x^2+3xy+2y^20 , то оно будет равносильно неравенству

$|x+y|-8\geq 0\\|x+y|\geq 8\\\left [ {{x+y\geq 8} \atop {x+y\leq -8}} \right. \\\left [ {{y\geq -x+8} \atop {y\leq -x-8}} \right.$

Рассмотрим уравнение:

$x(x-4)+y(y-2)=x^2-4x+4-4+y^2-2y+1-1=(x-2)^2+(y-1)^2-5\\(x-2)^2+(y-1)^2=a+5$

Это окружность с радиусом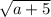 $\sqrt{a+5}$ и центром (2; 1). Изобразим это графически (см. рис. 1) Единственный случай, когда система имеет единственное решение, представлен на рисунке 1. При увеличении a окружность будет увеличиваться, и система будет иметь бесконечно много решений.

Радиус окружности перпендикулярен прямой y = -x + 8 и проходит через точку (2; 1). Значит, прямая, содержащая этот радиус, имеет вид y = x + m. Подставив x = 2, y = 1, получим m = -1. Найдём точку пересечения прямых y = x - 1 и y = -x + 8:

$x-1=-x+8\\2x=9\\x=4.5\\y=4.5-1=3.5$

Это точка (4,5; 3,5), то есть центр некоторого квадрата. Заметим, что радиус равен 2,5 диагоналям квадрата со стороной 1. Значит,

$\sqrt{a+5}=2.5\sqrt{2}\\a+5=6.25*2\\a=7.5$

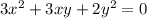2. Если 3x^2+3xy+2y^2=0 , то x = 0, y = 0. Тогда из уравнения следует, что a = 0. Тогда окружность будет иметь радиус 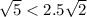$\sqrt{5}$ . Значит, с областью 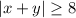$|x+y|\geq 8$ она не будет иметь пересечений, и в данном случае решение единственно (рис. 2).