При каких значениях а график функции у=ах ^-3) +2 проходит через точку а (-2; 1/8)

Ответы

safeon 13.01.2022 06:54

a=15

Объяснение:

подставим точку (-2; 1/8) в уравнение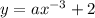 $y=ax^{-3}+2\\$

$1/8=a*\frac{1}{(-2)^{3} }+2\\-1.875=a*\frac{1}{-8}\\a=-1.875*-8\\a=15$

ПОКАЗАТЬ ОТВЕТЫ

kolyamusin01 24.01.2024 13:03

Для определения при каких значениях а график функции y = a(x^-3) + 2 проходит через точку (-2, 1/8), мы должны подставить координаты этой точки в уравнение функции и решить его относительно параметра а.

Сначала заменим x на -2 и y на 1/8:

1/8 = a((-2)^-3) + 2

Заметим, что (-2)^-3 = 1/(-2)^3 = 1/(-8) = -1/8, поэтому уравнение можно переписать следующим образом:

1/8 = a*(-1/8) + 2

Далее упростим уравнение:

1/8 = -a/8 + 2

Для начала, избавимся от знаменателей, умножив оба выражения на 8:

1 = -a + 16

Теперь выразим a:

-a = 1 - 16
-a = -15

Наконец, умножим оба выражения на -1, чтобы избавиться от отрицательного знака:

a = 15

Таким образом, при значении a = 15 график функции y = a(x^-3) + 2 проходит через точку (-2, 1/8).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра