Представьте многочлен в виде куба суммы или куба разности двух выражений: а^3+6a^2b+12ab^2+8b^3. выражения: u^3/8+3u^2v/2+6uv^2+8v^3. возведите в степень: (a+2b)^3
Ответы
Формула куба суммы и разности:
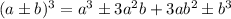
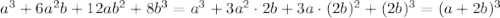
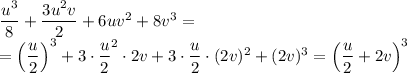
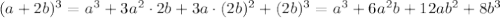
ПОКАЗАТЬ ОТВЕТЫ
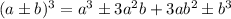
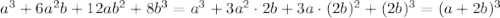
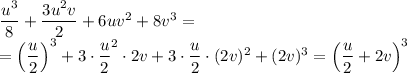
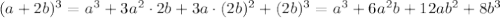
ответ ответ ответ ответ ответ ответ
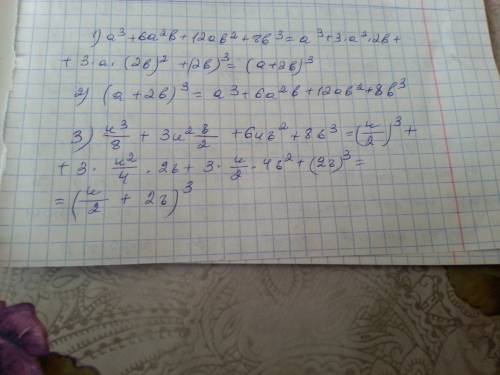
ПОКАЗАТЬ ОТВЕТЫ
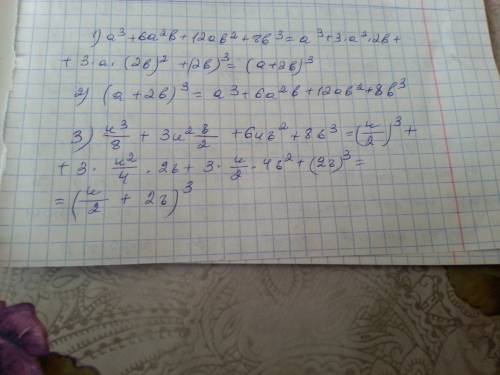
Другие вопросы по теме Алгебра
Популярные вопросы
- В какой строке от всех глаголов образуются только страдательные причастия,...
2 - Краткое описание картины с цезарем Убийство Цезаря...
3 - Відомо, що точки A, B, C і D — вершини прямокутника. Дано: A(0;0);B(0;1);C(8;1)Визнач...
2 - X(3x-2y)+(x+y)^2 упростите выражение...
2 - Напиишите сочинение на тему Менің сүйікті фантастикалық шығармам 15-20предложений...
1 - Әр жиында қанша элемент бар?а) көгенісә) жеміс6) сусынНені байқадың?...
1 - 5. В заводскую столовую доставили 0,96 т ово- щей. В первый день израсходовали...
3 - Чому Бодлера називали королем поетів ?...
1 - Добути сульфур(ІV) оксид і цинк оксид різними (трьома)...
3 - Про які моральні цінності йдеться в новелах?...
1