Представьте данный многочлен (2x + y )^2 +(2xy-1)^2 - (2x-y)^2 в виде произведения а) двух одинаковых многочленов; б) двух разных многочленов.
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько различных трехзначных чисел можно записать с цифр 0, 3, 5, 6, 9, если цифры...
1 - Оксид металічного елемента EOз масою 11бг повністю відновили воднем і добули метал...
2 - Прокоментуй рядки з повісті-казки Ю. Винничука Місце для дракона : Хто хоч краплю...
1 - План до біографії герберта уеллса....
1 - необходимо выполнить итоговую проверку по геометрии ставлю все свои (58)...
1 - Доказать тождество sin(a+п)/sin(a+(3п/2)) + сos(п-a)/cos(п/2+a)= 1/cosa...
3 - На вертикально-фрезерном станке требуется изготовить деталь. Составьте последовательность...
1 - По теореме виета: x^2 - 3x -5 = 0...
1 - Коли сталися зміни в суспільній свідомості щодо погляду на світ дитинства...
2 - 7. Кестеде оқушылардың математика пәнінен өткен емтиханның нәтижелері берілгенДұрыс...
2
Заметим, что члены с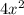 взаимоуничтожаются, тогда
взаимоуничтожаются, тогда
Члены с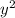 тоже взаимоуничтожаются,
тоже взаимоуничтожаются,
Также члены с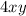 взаимоуничтожаются
взаимоуничтожаются
Заметим, что получился полный квадрат
Это произведение двух одинаковых многочленов.
Произведение двух разных многочленов может напишу через час.
(a + b)^2 = a^2 + 2ab + b^2
Применим эту формулу к первому слагаемому (2x + y)^2:
(2x + y)^2 = (2x)^2 + 2 * 2x * y + y^2 = 4x^2 + 4xy + y^2
Применим формулу квадрата суммы также ко второму слагаемому (2xy-1)^2:
(2xy-1)^2 = (2xy)^2 + 2 * 2xy * (-1) + (-1)^2 = 4x^2y^2 - 4xy + 1
Применим формулу квадрата разности к последнему слагаемому (2x-y)^2:
(2x-y)^2 = (2x)^2 - 2 * 2x * y + y^2 = 4x^2 - 4xy + y^2
Теперь сложим полученные результаты:
4x^2 + 4xy + y^2 + 4x^2y^2 - 4xy + 1 - (4x^2 - 4xy + y^2)
Удалим скобки и сгруппируем слагаемые:
4x^2 + 4x^2y^2 - 4x^2 + 4xy - 4xy + y^2 - y^2 + 1
Заметим, что некоторые слагаемые сокращаются:
4x^2 - 4x^2 = 0
4xy - 4xy = 0
y^2 - y^2 = 0
Осталось только слагаемое 1:
1
Таким образом, заданный многочлен (2x + y)^2 +(2xy-1)^2 - (2x-y)^2 представим в виде произведения двух одинаковых многочленов: 1.
б) Теперь представим данный многочлен в виде произведения двух разных многочленов.
Мы можем разложить каждое слагаемое и перемножить полученные многочлены:
(2x + y)^2 = (2x)^2 + 2 * 2x * y + y^2 = 4x^2 + 4xy + y^2
(2xy-1)^2 = (2xy)^2 + 2 * 2xy * (-1) + (-1)^2 = 4x^2y^2 - 4xy + 1
(2x-y)^2 = (2x)^2 - 2 * 2x * y + y^2 = 4x^2 - 4xy + y^2
Теперь перемножим полученные многочлены:
(4x^2 + 4xy + y^2)(4x^2y^2 - 4xy + 1)(4x^2 - 4xy + y^2)
Полученное выражение является произведением двух разных многочленов. В данном случае, дальнейшие сокращения сложны провести, и поэтому на данном этапе мы достигли оптимального ответа.
Таким образом, заданный многочлен (2x + y)^2 +(2xy-1)^2 - (2x-y)^2 представим в виде произведения двух разных многочленов, которые получены путем разложения и перемножения отдельных слагаемых.