1. Алгебра
  2. Постойте график функции у=((3х-2)^-5)^1/5

Постойте график функции у=((3х-2)^-5)^1/5 умоляю сделайте!

Valeria0710 Valeria0710    1   25.06.2019 11:50    2

Ответы
Dgukpd Dgukpd  02.10.2020 11:07

y=((3x-2)^{-5})^{\frac{1}{5} }\\\left \{ {{y=(3x-2)^{-1}} \atop {(3x-2)^{-5}\geq 0}} \right. \\\left \{ {{y=\frac{1}{3x-2} } \atop {\frac{1}{3^5*(x-2/3)^5} \geq 0}} \right. \\\left \{ {{y=\frac{1}{3(x-2/3)} } \atop {x-2/30}} \right. \\\left \{ {{y=\frac{1/3}{x-2/3} } \atop {x2/3}} \right.

Первоначальная функция имеет следующею область определения: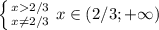 \left \{ {{x2/3} \atop {x\neq 2/3}} \right. x\in(2/3;+\infty)

Построим схематично преобразованную функцию Y и наложим ограничение. График функции Y это гипербола, которая лежит в 1 и 3 четвертях относительно следующих прямых: y=0; x=2/3, которые так же являются асимптотами. Пересечение с осями координат: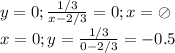 y=0;\frac{1/3}{x-2/3} =0;x=\oslash \\x=0;y=\frac{1/3}{0-2/3} =-0.5

См. вниз. (1)

Что бы понять как именно убывает функция найдём не сколько точек.

У получившейся кривой есть точка, которая равноудалена от двух асимптот точка A. См. вниз (2)

Найдём координаты этой точки и ещё пару точек кривой, чтобы понять как быстро функция убывает.

y=\frac{1/3}{x-2/3}\\y=x-2/3\\(x-2/3)^2=1/3\\3x^2-4x+\frac{4-3}{3}=0;D=16-4=12\\x=\frac{2\pm \sqrt{3} }{3}

Существует только x>2/3.

\frac{2+\sqrt{3} }{3}-\frac{2}{3} =\frac{\sqrt{3} }{3}\\A(\frac{2+\sqrt{3} }{3};\frac{\sqrt{3} }{3})

y=\frac{1/3}{x-2/3}\\1.y(3)=\frac{1/3}{7/3} =1/7\\x=\frac{1/3}{y} +2/3\\2.x(1.5)=\frac{1/3}{3/2} +2/3=8/9

Для ясности нарисую табличку.

См. вниз (3)

Теперь строим график нашей функции.

См. вниз (4)


Постойте график функции у=((3х-2)^-5)^1/5 умоляю сделайте!
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
MrMixa008 MrMixa008  22.06.2019 06:00
Найдите площадь квадрата описанного вокруг окружности радиуса 18...
Diana111111112 Diana111111112  22.06.2019 06:00
1000x³-(10x-1)(100x²+10x+1)+x+6= якщо, х =1,147...
dina2607 dina2607  22.06.2019 06:00
Найдите производную функции f(x)=9x^6, f(x)=1/11x^-11,...
Littlebybigheart1111 Littlebybigheart1111  22.06.2019 06:00
8класс. решить, . 1)турист км по шоссе и 6 км по проселочной дороге, затратив на весь путь 2 ч. по шоссе он со скоростью на 2 км/ч больше, чем по проселочной дороге. с какой скоростью...
k456789 k456789  22.06.2019 06:00
Найдите первый член прогрессии, если s=40 q=1/3...
UzZzeR UzZzeR  22.06.2019 06:00
Длина прямоугольника больше ширины на 4 см,а его площадь равна 96 см2. найдите стороны прямоугольника....
mockingbird12 mockingbird12  24.07.2019 21:20
Дана арифметическая прогрессия 3; 5; 7; найдите её восьмой член....
Delikmarkomer Delikmarkomer  24.07.2019 21:20
Решите уравнение, 7 класс 4q^2+3q=0...
ayska1 ayska1  24.07.2019 21:20
Найдите значение выражения 0,2а^4 х^n * (-5)а^2 х...
rgmabbasov rgmabbasov  10.09.2020 23:56
1.числовая последователность (xn) выражена так: a) xn=3,4 -1,6nb)x1=1, xn+1=(-1)^n*xn=2c)x1=2, x2=1, xn+2=3xn+1-xn/2найдите последовательность 5ого члена х5​...

Популярные вопросы