Почему в данном случае обе части уравнения нельзя делить на cosx? 2cosxsinx= $\sqrt{2}$ cosx

Ответы

FoxyDi 10.10.2020 05:11

$2cosx\cdot sinx=\sqrt2\cdot cosx$

Если уравнение делить на cosx, то надо оговориться, что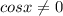 $cosx\ne 0$ , так как на 0 делить нельзя. В силу этого можно потерять корни уравнения, при которых cosx обращается в 0, это $x=\frac{\pi}{2}+\pi n,\; n\in Z$ . Тогда надо отдельно проверить, не являются ли $x=\frac{\pi}{2}+\pi n,\; n\in Z$ корнями заданного уравнения, подставив их в это уравнение.

$2cosx\cdot sinx=\sqrt2\cdot cosx\; |:cosx\ne 0\; \to \; x\ne \frac{\pi }{2}+\pi n,\; n\in Z\\\\2sinx=\sqrt2\; \; \to \; \; sinx=\frac{\sqrt2}{2}\; ,\; \; x=(-1)^{n}\cdot \frac{\pi}{4}+\pi k,\; k\in Z\\\\x=\frac{\pi}{2}+\pi n:\; \; 2cos(\frac{\pi}{2}+\pi n)\cdot sin(\frac{\pi}{2}+\pi n)=\sqrt2\cdot cos(\frac{\pi}{2}+\pi n)\; ,\\\\2\cdot 0\cdot (\pm 1)=\sqrt2\cdot 0\; ,\\\\0=0$

Так как получили верное равенство, то $x=\frac{\pi}{2}+\pi n$ являются корнями заданного уравнения.

$P.S.\; \; \; \; sin(\frac{\pi}{2}+\pi n)=\left [ {{sin(\frac{\pi}{2}+2\pi n)=+1\; ,} \atop {sin(\frac{3\pi}{2}+2\pi n)=-1\; .}} \right.$

Чтобы не проводить лишнюю проверку , при решении уравнения надо просто вынести общий множитель cosx за скобку, тогда сразу получим две серии решений:

$2\, cosx\cdot sinx-\sqrt2\cdot cosx=0\\\\cosx\cdot (2\, sinx-\sqrt2)=0\; \; \Rightarrrow \\\\cosx=0\quad ili\quad \; \; 2\, sinx-\sqrt2=0\\\\x=\frac{\pi }{2}+\pi n\; ,\; n\in Z\quad ili\quad sinx=\frac{\sqrt2}{2}\; ,\; \; x=(-1)^{k}\cdot \frac{\pi}{4}+\pi k\; ,\; k\in Z\\\\Otvet:\; \; x=\frac{\pi }{2}+\pi n\; ,\; \; x=(-1)^{k}\cdot \frac{\pi}{4}+\pi k\; ,\; \; n,k\in Z\; .$