1. Алгебра
  2. Периметр прямоугольника равен

Периметр прямоугольника равен p. при каких размерах сторон его площадь будет наибольшей?
50 ! ​

Коtик Коtик    3   09.12.2019 23:10    2

Ответы
lisa1003 lisa1003  10.10.2020 19:40

P=2(a+b)=2a+2b\; \; ,\; \; 2a=P-2b\; ,\; \; a=\frac{P}{2}-b\\\\S=ab=(\frac{P}{2}-b)\, b=\frac{P}{2}\cdot b-b^2\\\\S'=\frac{P}{2}-2b=0\; \; \to \; \; 2b=\frac{P}{2}\; \; ,\; \; b=\frac{P}{4}\\\\a=\frac{P}{2}-b=\frac{P}{2}-\frac{P}{4}=\frac{P}{4}\; \; \Rightarrow \; \; \; a=b=\frac{P}{4}

Если стороны прямоугольника равны, то есть прямоугольник является квадратом, и сторона квадрата равна четвёртой части от периметра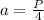  a=\frac{P}{4} , то площадь прямоугольника будет наибольшей.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
DrYgAn8998 DrYgAn8998  30.05.2019 23:04
Разложите многочлен на множители 4xy в квадрате -16x...
svetlana278 svetlana278  30.05.2019 23:01
3x=21 16x=-4 две третих x=14 -0,2x=-0,3 -5x=45 18x=-6 3x+2=14x-75 2x-1=3x+99 7x-4=x-16 13-5x=8-2x решите ....
viktoriy2009 viktoriy2009  31.05.2019 00:50
Поиск результатов по фразе между лисой и зайцем - 10 метров. когда лиса поймает зайца, если она бежит со скоростью 8м\с. а он со скоростью 7 м\с?...
nikmeldov nikmeldov  31.05.2019 00:50
Длину прямоугольника увеличили на 15 процентов, ширину на 12. насколько увеличилась площадь ?...
alexalevdorovic alexalevdorovic  09.03.2019 14:10
Доходный налог составляет 13% от заработной платы. после удержания налога в.и. получил 11310 руб. сколько руб. составляет его заработная плата...
yuliav1801 yuliav1801  09.03.2019 14:10
3tg (в квадрате) x- корень из 3tgx= 0...
kiraueus kiraueus  09.03.2019 14:20
Из формул для вычесления высоты равностороннего треугольника a√3 h= выразите сторону a 2...
mindrehumor11111 mindrehumor11111  09.03.2019 14:20
Бригада должна была изготовить определённое количство стульев за 10 дней. однако она ежедневно изготавливала на 20 стульев больше, чем планировала превоначально, поэтому за...
zvezda026 zvezda026  09.03.2019 14:20
Верно ли равенство(2*4 /9-5 /9)*18 /17=(1*1 /2+13 /10): 1*2 /5...
Алахахбар228 Алахахбар228  09.03.2019 14:20
Выразите из формулы q=mc(t-p) переменную p...

Популярные вопросы