Периметр прямоугольника равен 76 см. найди стороны прямоугольника, если он имеет наибольшую площадь.

Ответы

shamil20042 09.06.2020 06:41

1-ый вариант.

Прямоугольник будет иметь наибольшую площадь, если его стороны будут равны. Как нам известно, периметр- сумма длин всех сторон. Пусть сторона-a, тогда:

$P=4\,a\\76\,cm=4\,a\\a=76\,cm:4\\a=19\,cm$

Для больше убедительности можем найти площадь:

$S=a^2\\S=19^2\,cm^2\\S=361\,cm^2$

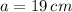
ответ: $a=19\,cm$

2-ой вариант.

Длина- a cm

Ширина- (38-a) cm

Теперь, по условию задачи зададим график функции:

f(x)=a(38-a)=38a-a^2

Найдём производную данной функции, приравняем её к нулю, так мы получим точки экстремума.

$f'(x)=38-2a\\38-2a=0\\19-a=0\\a=19\\\\_{-------}^{\quad\quad +} \circ _{-------}^{\quad\quad-}_$

Переход идёт от плюса к минусу, а это значит, что в этой точке функция принимает наибольшее значение, вернёмся в первоначальное условие и выясним, что длина и ширина равны.

ответ: 19 см

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра