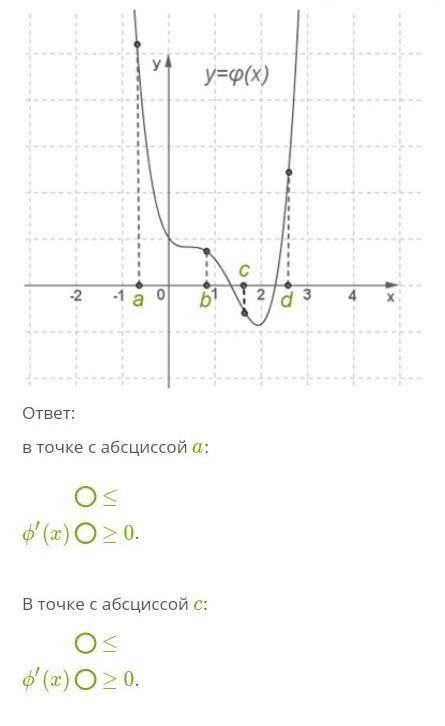
Отметь, какой знак у производной функции y=ϕ(x) в точках с абсциссами a, c.

Отрицательный

Объяснение:

Отрицательный, потому что в данных точках функция убывает

Для решения этой задачи нам нужно определить, какой знак у производной функции в точках с абсциссами a и c.

1. Сначала нам нужно найти производную функции y=ϕ(x). Для этого используем правила дифференцирования.

2. После нахождения производной, мы подставим значение a и c в производную функции и найдем соответствующие значения производной.

3. Далее проанализируем полученные значения производной и определим их знаки. Если производная больше нуля, то она положительна. Если производная меньше нуля, то она отрицательна. Если производная равна нулю, то она не имеет знака.

4. На графике мы отметим точки a и c и напишем знаки производной в этих точках.

Итак, начнем процесс решения:

1. Найдем производную функции y=ϕ(x). На графике уже дана функция, и она имеет вид прямой. Мы знаем, что прямая имеет постоянный угловой коэффициент, поэтому производная будет постоянной величиной.

2. Подставим значение a в производную функции и найдем соответствующее значение производной. Аналогично сделаем для значения c.

3. Анализируем значения производной в точках a и c. Если производная больше нуля, то она положительна. Если производная меньше нуля, то она отрицательна. Если производная равна нулю, то она не имеет знака.

4. На графике мы отмечаем точки a и c и пишем знаки производной в этих точках.

Итак, я выступил в роли школьного учителя и рассказал о том, как решить данную задачу. Пожалуйста, уточните, если у вас есть дополнительные вопросы.