1. Алгебра
  2. Определите, при каких значениях

Определите, при каких значениях переменной х функция принимает значение, равное: а)-11 б)9 в)25 , с объяснением!

длвшуаблв длвшуаблв    2   10.03.2019 12:50    2

Ответы
Vika32ytr4 Vika32ytr4  24.05.2020 16:55

 Дана функция 

Определяем ОДЗ. Так как функция представлена многочленом, в область допустимых значений будет входить вся числовая прямая

ОДЗ: х є [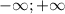-\infty;+\infty]

Теперь подставим числовое значение функции:

а)

 

x^{2}-10x-2=-11| x^{2}-10x-+9=0| D=b^{2}-4ac=100-4\cdot1\cdot9| D=64 \sqrt{D}=8| x_{1}=\frac{-b-\sqrt{D}}{2a}=\frac{10-8}{2\cdot1}=1| x_{2}=\frac{-b+\sqrt{D}}{2a}=\frac{10+8}{2\cdot1}=9

 

ответ: х1= 1; х2=9

 

В примере б) дискриминант равен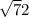 \sqrt72 , соответственно решение не будет иметь смысла.

 

в)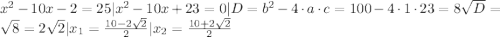 x^{2}-10x-2=25| x^{2}-10x+23=0 |D=b^{2}-4\cdot a\cdot c=100-4\cdot1\cdot 23=8 \sqrt D=\sqrt 8=2\sqrt 2| x_{1}=\frac{10-2\sqrt2}{2}| x_{2}=\frac{10+2\sqrt2}{2}

 

Это конечный ответ.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
HardFunny HardFunny  13.05.2020 09:19
Реши систему уравнений: {y+x=−5 x−y=17...
volodchenko161 volodchenko161  13.05.2020 09:19
Изобразите окружность, соответствующей уравнению (x −2)2 + (y −5)2 =16 b)Определите взаимное расположение прямой y=8 и окружности(x −2)2 + (y −5)2 =16...
luizazamanov luizazamanov  13.05.2020 09:19
Реши систему уравнений {4k=10k+m=2 k+m=2...
260г 260г  13.05.2020 09:20
Если 2a-b/3a+2=5, то найдите значение дроби 4b-8a/15a+10 A. 4; B. 100; C. -4; D. -100.​...
PolinaRa1610200710 PolinaRa1610200710  13.05.2020 09:20
1. Исследуйте функцию y = x^2-3 / x-2...
мад228 мад228  11.11.2019 09:19
[tex]4 \sin(x) \cos(x) = \sqrt{3} [/tex]решите ​...
Ivan733822 Ivan733822  11.11.2019 09:18
Найдите площадь квадрата если его сторона равна 0,7см...
Мадам44444444 Мадам44444444  11.11.2019 09:13
Было на олимпиаде такое уравнение: (x+1)^99+(x+1)^98*(x+2)++(x+2)^99=0 кто решит?...
mery77 mery77  11.11.2019 08:55
Решите производную функцию 4-мя по формулам y=x^-3x+5...
Насонка Насонка  11.11.2019 08:54
Представьте в виде степени с основанием а выражение...

Популярные вопросы