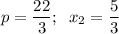Один из корней уравнения x²+px-15=0 равен -9.Найдите второй корень и коэффициент p
Другие вопросы по теме Алгебра
Популярные вопросы
- 3.в какой работе по охране водных обитателей могут учавствовать...
1 - Где находится тюльпанавое дерево и клад в рассказе золотой жук...
3 - Звуко буквеный разбор слова пестолет...
3 - Выразите : в арах 5 км квадратных 13 га выразите.: в гектарах и...
3 - Вычислить: sin(п/4-a), если sina=корень из 2/3, п/2 a п...
3 - Яизрыл всю землю сделал ее неровной кто я...
1 - Три четвёртых кг конфет стоят одну целую четыре пятых тысяч рублей,...
3 - Рабочим выделили для садовых участков 6 га земли. сколько рабочих...
3 - Проволоку сопротивлением 25 ом разрезали на 5 одинаковых частей...
1 - Спиши вставляя пропущенные падежные окончания пошел он к своей землянк...
2
Решение и ответ:
Найдём коэффициент p, подставив значение x₁ = -9 в уравнение:
Определим второй корень уравнения x₂, подставив найденный коэффициент p в исходное уравнение:
ответ: