. Обязательно с решением. Умоляю
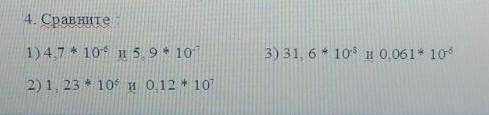
Другие вопросы по теме Алгебра
Популярные вопросы
- Ребята выполнить технический рисунок/чертёж....
3 - сделать таблицу по географии Океаны Земли 7 столбиков 1 столбик:...
2 - По черчению надо рассчитать...
1 - Определи вид глаголов и заполни таблицу. положить класть искать...
2 - Почему,изображая Татьяну-знатную петербургскую даму,княгиню,Пушкин...
2 - Вкладчик поместил в банк 1256 р. Банк ежегодно выплачивает вкладчику...
3 - Подскажите супер качевую музыку....
3 - Налоги, взимавшие со скотоводов-кочевников...
2 - Контрольна робота з теми дружба і кохання, до тьь...
2 - Определить массу оксида натрия, которую можно получить при сгорании...
3
В решении.
Объяснение:
Сравнить:
1) 4,7*10^-6 и 5,9*10^-7;
4,7*10⁻⁶ и 5,9*10⁻⁷;
1/4,7⁶ и 1/5,9⁷;
1/4,7⁶ > 1/5,9⁷;
Чем больше знаменатель, тем меньше значение дроби.
2) 1,23*10^6 и 0,12*10^7;
1,23*10⁶ и 0,12*10⁷;
Привести второе число к стандартному виду:
1,23*10⁶ и 1,2*10⁶;
1,23*10⁶ > 1,2*10⁶;
Если показатели степени одинаковые, больше то число, основание которого больше.
3) 31,6*10^-8 и 0,061*10^-8;
31,6*10⁻⁸ и 0,061*10⁻⁸;
1/31,6⁸ и 1/0,061⁸;
Привести оба знаменателя к стандартному виду:
1/3,16⁹ и 1/6,1⁶;
1/3,16⁹ < 1/6,1⁶;
Чем больше знаменатель, тем меньше значение дроби.