Объясните, почему уравнение дает один корень и как это понять?

у=х^5 это кубическая парабола

у=х+4 это прямая

точка пересчения параболы и прямой будет одна А (х:у) , где х - есть корень ур-я

Попробую аналитически:

Предположим обратное: данное уравнение имеет по меньшей мере 2 корня. Пусть это числа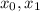 ; Без потери общности будем считать, что 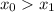; Тогда пара (x₀;x₁) является решением системы: ; Вычтем из одного уравнение второе. Получим: 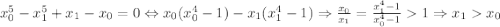, противоречие. (отдельно заслуживают внимания такие моменты как возможность x0,1=0 и т.д, но это все невозможно, т.к x+4 не проходит через подобные точки).

Итак, значит уравнение имеет не более одного корня