Объясните , каков принцип решения таких задач. Функція f є парною. Чи може виконуватися рівність:

1)

2)

3)

Відповідь обґрунтуйте.

Ответы

margusqw 22.07.2022 17:31

Функция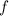 называется парной, если:

$f(x)=f(-x)\;\;,\;\;x\in D(f)$

Учитывая это попробуем узнать, могут ли выполняться равенства:

1)~f(2)-f(-2)=1

Поскольку по условию функция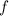 парная, то:

f(2)=f(-2)

Любое число минус это же число = 0. Значит равенство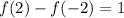 f(2)-f(-2)=1 выполняться не может. Можно это доказать. Пусть 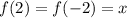f(2)=f(-2)=x , тогда:

$x-x=1\;\;\Rightarrow\;\;0=1$ - не верно. Следовательно, уравнение не имеет корней и f(2)-f(-2) не может быть равно единице.

$2)~f(5)\cdot f(-5)=-2$

Поскольку по условию функция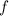 парная, то:

f(5)=f(-5)

При умножении двух равных чисел не может получиться отрицательное число. Потому что при умножении положительных чисел получается положительное число, и при умножении отрицательных чисел также получается положительное число. То есть:

$(+)\cdot(+)=(+)(-)\cdot(-)=(+)$

Значит равенство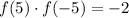 $f(5)\cdot f(-5)=-2$ выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть 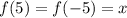f(5)=f(-5)=x , тогда 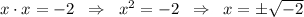$x\cdot x=-2\;\;\Rightarrow\;\;x^2=-2\;\;\Rightarrow\;\;x=\pm\sqrt{-2}$ корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и 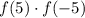$f(5)\cdot f(-5)$ не может быть равно -2.

$3)\dfrac{f(1)}{f(-1)}=0$

Поскольку по условию функция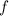 парная, то:

f(1)=f(-1)

При делении равных чисел результат всегда равен 1. Значит равенство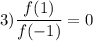 $3)\dfrac{f(1)}{f(-1)}=0$ выполняться не может. Доказательство:

Пусть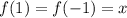 f(1)=f(-1)=x , тогда 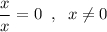$\dfrac{x}{x}=0\;\;,\;\;x\ne0$ . Домножим обе части уравнения на x, тогда 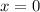x=0 , что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и 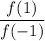$\dfrac{f(1)}{f(-1)}$ не может быть равно 0.