,нужны оба варианта формулы сокращенного цмножения
Другие вопросы по теме Алгебра
Популярные вопросы
- Суицыдники перерождаються? Да нет?...
2 - Выпишите сравнения метафоры и эпитет Внизу глубоко подо мнойПоток усиленный...
3 - Що при паралельному проектуванні прямокутника не можна отримати? ...
1 - тело движется с горя под углом 60 градусов с ускорением 4м\с в квадрате...
3 - ответить на вопросы по тексту: Extensive research was carried out in...
2 - Озёра, как и люди, имек схои судьбы и хора Озеро Сентани находится в...
1 - Проверочная работа по теме: Религия восточных славян 6 класс...
2 - Чем взрослые насекомые тутового шелкопряда отличаются от бабочки крапивницы...
2 - Кому з героїв твору належить висловлювання стосовно Козацької фортеці:...
2 - Деревообрабатывающий комбинат направил строительной организации уведомление...
2
Вариант 1
Задание 1
а)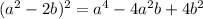
б)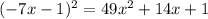
в)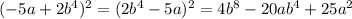
г)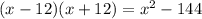
д)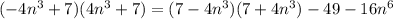
Задание 2
а)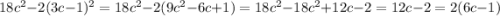
б)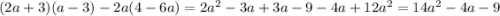
в)
Задание 3
а)
б)
Вариант 2
Задание 1
а)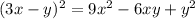
б)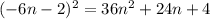
в)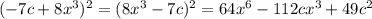
г)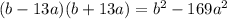
д)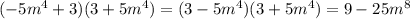
Задание 2
а)
б)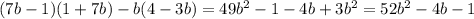
в)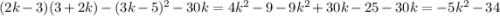
Задание 3
а)
б)