Нужно выразить I, I1, I2, I3
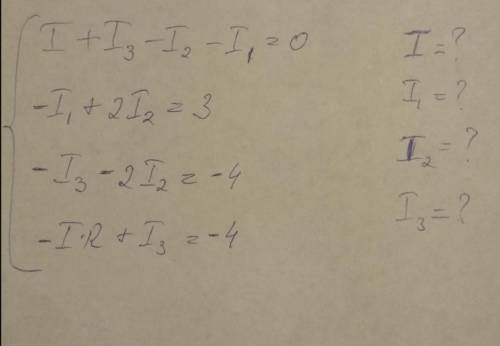
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить цитатный план по стихотворению отрар...
2 - очень надо Укажите имя существительное женского рода: 1) картофель 2)...
3 - 1. Выполни задание в тетради: -составь схему «Транспорт веществ у...
3 - До ть вже будь-ласка , хотя би 1 завдання...
1 - Написать эссе на тему Чему учат былины. даю...
2 - 63 бет, 3-тапсырма. Прочитай сказку, пойми содержание и ответь на вопросы...
1 - А Мәтін мазмұнына сәйкес кестені толтырыңдар. Орналас-Атауықан жеріҚытайКереметтүріСалыну...
2 - 6 3/7саны координаталық сәуледе қандай натурал сандардың арасында орналасқан?...
1 - 1. На прямой отметьте последовательно три точки М, N и K, и точку Е не...
2 - Физический диктант: Скорость обозначается – Время обозначается – Единица...
2
Объяснение:
К уравнению 1, умноженное на (-1), прибавляем уравнение 2:
К уравнению 1, умноженное на 2, прибавляем уравнение 3, умноженное на 3:
К уравнению 1 прибавляем уравнение 4, умноженное на 5:
Чтобы записать 4-ю строку в целых числах - умножим её на 5:
Решаем методом Гаусса.
К уравнению 4 прибавляем уравнение 1, умноженное на 24:
К уравнению 4 прибавляем уравнение 2, умноженное на -24:
К уравнению 4 прибавляем уравнение 3, умноженное на -36:
ответ: I=1 I₁=0,2 I₂=1,6 I₃=0,8.