нужно
Там где не видно написано
х-4/5 меньше
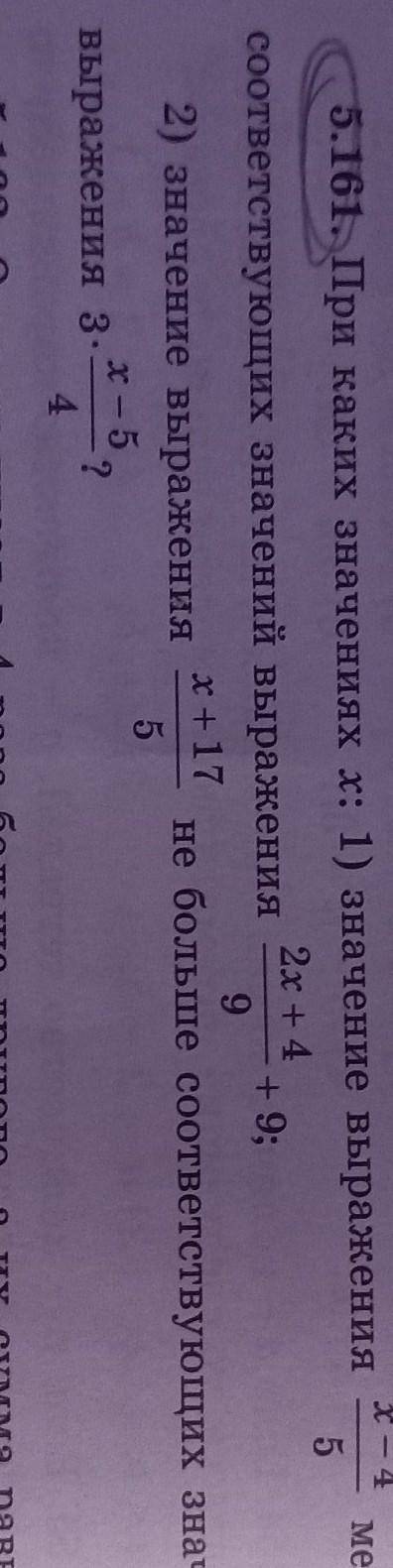
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишите глаголы,которые оканчиваются на -чь.10 глаголов. например-...
2 - Какие расстения есть в санкт-питербурге...
1 - Сочинение наказание президенту российской федерации...
2 - Скосили 32% луга, после чего осталось скосить ещё 136га.найдите площадь...
1 - Этанол и глицерин при обычных условиях - жидкость?...
1 - Вставь слова. пiд час розмови необхiдно i добирати слова. i викладати...
2 - Морфологический разбор слова подплыл к берегу...
3 - Написать рассказ о том что я понимаю что такое доброе дело и дарить...
3 - 10. укажите предложения, в которых вводные слова и словосочетания...
1 - Составь памятку для винни-пуха как вести себя в гостях...
1
В решении.
Объяснение:
1) (х - 4)/5 < (2х + 4)/9 + 9
Умножить все части неравенства на 45, чтобы избавиться от дробного выражения:
9*(х - 4) < 5*(2x + 4) + 45*9
9x - 36 < 10x + 20 + 405
9x - 10x < 425 + 36
-х < 461
x > -461
При х > -461 первое выражение меньше второго.
2) (х + 17)/5 = 3(х - 5)/4
Умножить все части уравнения на 20, чтобы избавиться от дробного выражения:
4*(х + 17) = 5*3(х - 5)
4х + 68 = 15х - 75
4х - 15х = -75 - 68
-11х = -143
х = -143/-11
х = 13.
При х = 13 первое выражение не больше второго (равно ему).