Нужно понятное решение
(10 кл.)
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие предложение называются простыми,а какие - сложными?...
2 - Спільнокореневі слова до слова бетонний...
1 - Нужно дописать предложения, включив в предложения причастные обороты....
3 - Составьте полное ионное уравнение: al2(so4)3 + ba(oh)2= ba(no3)2 + k3po4=...
1 - Когда разливается река сена и почему?...
2 - 1.органоид клетки, в котором происходит фотосинтез это: 1)хромопласты...
1 - Составьте развёрнутый план для сообщения по теме общение в жизни людей...
3 - Машина в первый день приехала 750 км, что составило 30% всего пути.какой...
2 - Решите : ) разложите на множители: а+ а ( в квадрате - во второй степени)...
1 - Периметр треугольника равен 36 см. стороны пропорциональны числам 3,...
3
1)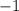 ,
, 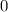 ,
,  .
.
2)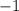 ,
, 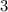 .
.
Объяснение:
1) По утверждению, обратному лемме Ферма, в точке экстремума функции значение её производной равно нулю. Отсюда следует, что для нахождения точки экстремума функции следует сначала найти производную функции, а затем найти точки, в которых она равна нулю. Они и будут являться точками экстремума исходной функции.
Для данной функции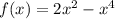 найдём производную:
найдём производную:
Решим теперь уравнение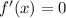 :
:
Отсюда следует, что или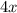 равно нулю, или
равно нулю, или 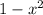 равно нулю.
равно нулю.
Первое:
Второе:
Получается, что точками экстремума функции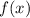 являются
являются 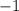 ,
, 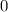 и
и  .
.
2) Аналогично первому заданию, для данной функции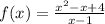 найдём производную:
найдём производную:
Решим теперь уравнение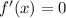 :
:
Из него следует, что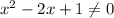 , а также
, а также 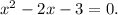
Для первого:
Для второго:
Все удовлетворяют условию
удовлетворяют условию 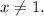
Получается, что точками экстремума функции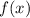 являются
являются 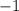 и
и 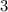 .
.