Нужна по решению систем нелинейных уравнений.9 класс 5 Вариант .В основном нужно решить 3,4,5.Неполные ответы идут мимо

Нужна по решению систем нелинейных уравнений.9 класс 5 Вариант .В основном нужно решить 3,4,5.Неполн

Ответы

Настена112132 29.06.2021 15:32

Объяснение: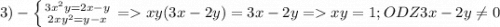 $3)-\left \{ {{3x^2y=2x-y} \atop {2xy^2=y-x}} \right. = xy(3x-2y)=3x-2y =xy=1 ;ODZ3x-2y\neq 0$ это первый шаг теперь второй 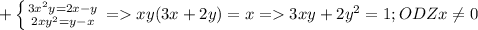$+\left \{ {{3x^2y=2x-y} \atop {2xy^2=y-x}} \right. = xy(3x+2y)=x =3xy+2y^2=1 ; ODZx\neq 0$ теперь из первого уравнения xy=1 подставим во второе 3*1+2y²=1 => y²=-1 что не может быть остальные случаи я тоже рассмотрел там выходит тоже самое а значит нет решений ; 4) здесь же можно сразу собрать в формулу 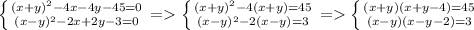$\left \{ {{(x+y)^2-4x-4y-45=0} \atop {(x-y)^2-2x+2y-3=0}} \right.=\left \{ {{(x+y)^2-4(x+y)=45} \atop {(x-y)^2-2(x-y)=3}} \right. =\left \{ {({x+y)(x+y-4)=45} \atop {(x-y)(x-y-2)=3}} \right.$ рассмотрим вторую систему и случаи при которых равенство верное их всего 2 а остальные два не подходят тогда в первом 1) x-y-2=1 x-y=3 подходит так как x-y=3 ; x-y=3 2) x-y-2=-3 x-y=-1 что тоже подходит теперь их нужно проверить подставим в первую систему x-y=3 => x=y+3 мы получим 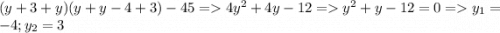(y+3+y)(y+y-4+3)-45=4y^2+4y-12 = y^2+y-12=0=y_1=-4 ;y_2=3 тогда первое решение (-1;-4) второе (6;3) теперь рассмотрим второй случай когда x=y+1 подставим и решим 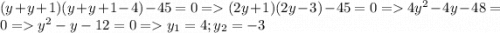(y+y+1)(y+y+1-4)-45=0 =(2y+1)(2y-3)-45=0 =4y^2-4y-48=0=y^2-y-12=0 = y_1=4;y_2=-3 получим третье решение (5;4) и четвертое (-2;-3) пятое задание на фото