Некто сказал другу: "дай мне 100 рублей,и я буду вдвое богаче тебя".друг ответил: "дай ты мне только 10 рублей и я стану в 6 раз богаче тебя".сколько денег было у каждого?
Другие вопросы по теме Алгебра
Популярные вопросы
- Дроби пятый класс,сколько будет 12 2/9-5 7/9...
1 - написать небольшой рассказ о Россий,который должен включать слова...
2 - Отзыв на рассказ А. В. Жвалевский, Е. Б. Пастернак. «Радость жизни»...
3 - Укажіть крайню точку північної Америки над...
2 - ,,спілка рудих,, яким чином Холмс досліджував місцевість поблизу контори...
2 - На тележку массой 200 кг,движущуюся со скоростью 10 м/ падает груз...
2 - До ть будь ласка історія ...
3 - Определить скорость движения поезда, если известно, что ведущее колесо...
1 - Прочитайте уривок. Випишіть з нього дієприкметники й віддієслівні...
3 - До ть контрольна робота з англійської мови...
3
Пусть у Некто х рублей, а у его друга - у рублей. Некто сказал другу, что если друг даст 100 рублей, то он вдвое богаче друга, то есть, имеем уравнение: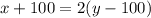
Тогда друг ему ответил: "Если дашь 10 рублей, то я стану в 6 раз богаче тебя", то есть, уравнение: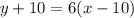
Решим систему уравнений:
А у Некто денег: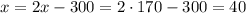 рублей.
рублей.
ответ: у Некто 40 рублей и у друга 170 рублей