не получается вообще

Докажите тождество (x²+y²)(z²+t²)=(xz-yt)²+(yz+xt)²

Объяснение:

(x²+y²)(z²+t²)=(xz-yt)²+(yz+xt)²

Преобразуем левую и правую часть:

(x²+y²)(z²+t²) = x²z²+x²t²+y²z²+y²t²

(xz-yt)²+(yz+xt)²= x²z²-2xzyt+y²t²+y²z²+2yzxt+x²t² = x²z²+y²t²+y²z²+x²t²

x²z²+x²t²+y²z²+y²t²= x²z²+y²t²+y²z²+x²t²

Тождество доказано.

1)  В левой части выполняем преобразования:  

(Сначала вычтем выражение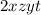 , а затем его же прибавим:)

(В первых скобках квадрат разности, а во вторых - квадрат суммы:)

2) Получили в левой части такое же выражение, что и в правой части:

Доказано.