Найти sin2x, если cosx=3/5, x ∈(0; п/2)
Ответы
Т.к. x ∈(0;П/2), то sinx>0
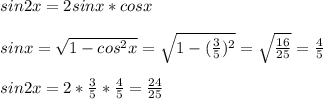
ПОКАЗАТЬ ОТВЕТЫ
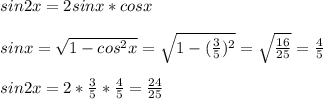
Другие вопросы по теме Алгебра
Популярные вопросы
- Сообщества по рождению и по месту жительства...
3 - Несколько традиций разных стран мира....
2 - Для функции y=x^2 найдите наименьшее на отрезке [-4; 2]...
1 - Скласти діалог хлопчика з водієм таксі...
3 - Сколькими различными можно разложить натуральное число n на сумму трёх...
1 - Решите уравнение. раскрывая скобки конечно же. 1)7(2+у)-3y=5y-6 2)-3(5a-1)+4a=2a+7(5-3a)...
3 - Какие тела изготовленные из а) алюминия б) меди.?...
1 - Сколько корней имеет уравнение x^2-x+3...
3 - Краткое содержание главные герои произведения александра сергеевича...
1 - Сообщества с рождения и по месту жительства...
3