1. Алгебра
  2. найти производную сложной

найти производную сложной функции: ln(e^2x+sqr(e^4x+1))

алибекalmaiurbrhje алибекalmaiurbrhje    1   14.04.2019 23:16    0

Ответы
slavaapakinp00lrn slavaapakinp00lrn  29.05.2020 12:18
Используем правила для нахождения производной сложной функции, суммы функций и табличные производные.
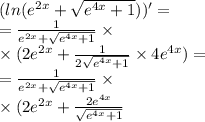
( ln( {e}^{2x} + \sqrt{ {e}^{4x} + 1} ) )^{ \prime} = \\ = \frac{1}{ {e}^{2x} + \sqrt{ {e}^{4x} + 1 } } \times \\ \times (2 {e}^{2x} + \frac{1}{2 \sqrt{ {e}^{4x} + 1}} \times 4 {e}^{4x} ) = \\ = \frac{1}{ {e}^{2x} + \sqrt{ {e}^{4x} + 1 } } \times \\ \times (2 {e}^{2x} + \frac{2 {e}^{4x} }{\sqrt{ {e}^{4x} + 1}}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kovalenko171019 kovalenko171019  22.05.2019 00:00
Как доказать, что если a+b c и d+e c, то (a+b+d+e)/2 c...
bogdansoroka20 bogdansoroka20  22.05.2019 00:00
1.найти cos2a, если cosa = 1/3. 2.напишите уравнение касательной к функции y=x-2x^2+1, в точке x0=-1. 3.найдите критические точки функции g(x)= корень из х - х...
Котик2525 Котик2525  21.05.2019 22:38
Из двух пунктов расстояние между которыми 54 км, выехали одновременно навстречу друг другу два велосипедиста и встретились через 2 часа.определите скорость каждого велосипедиста, если...
kotic13 kotic13  22.05.2019 00:00
Найдите наибольшее значение выражения3х^2-8ху+2у^2,если у-х=1...
lamsjsj lamsjsj  22.05.2019 00:00
Решите уравнение (x-5) (x+5)=(x-3)-во 2 степени +2...
Parf21 Parf21  21.05.2019 22:33
Вкоробке лежат сладкие и соленые конфеты. сколько соленых конфет в коробке, если вероятность вынуть такую конфету составляет 7/23 , а количество сладких конфет - 48....
korolovk korolovk  22.12.2020 20:59
При якому/найбільшому цілому значенніфункція у = (8-3n)x - 7 є зростаючою?​...
igubanova igubanova  22.12.2020 20:59
Чому дорівнює інтеграл від 2 до 1 f(x)dx,якщо інтеграл від 1 до -1 f(x)dx=2, інтеграл від 2 до -1 f(x)dx= -3​...
SnopcovaAlina07 SnopcovaAlina07  22.12.2020 20:59
решить надовычислите: cos²15° - sin²15°​...
KageyamaT KageyamaT  22.12.2020 20:58
построить на координатной плоскости...

Популярные вопросы