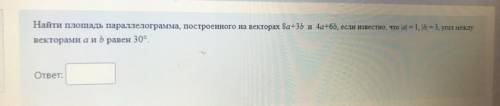
Найти площадь параллелограмма

Объяснение:

векторное произведение ab=1*3*sin30°=1,5

S=I(8a+3b)(4a+6b)I=I32a²+48ab+12ab+18b²I=I48ab+12baI=I48ab-12baI=

=I36abI=I36*1,5I=54 кв.ед.

Модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах. Поэтому  найдем сначала векторное произведение , а потом его модуль.  над всеми векторами стрелка сверху.  

(8а+3b)x(4a+6b)=32axa+48axb+12bxa+18bxb=32*0+48axb-12axb+18*0=  

36axb=36*1*3*sin30°=36*1*3*0.5=54  

I54I=54/кв. ед./  

использовал свойства векторного  произведения  

axa=0; bxb=0; bxa=-axb  

axb=IaI*IbI*sinα, где α- угол между векторами а и b  

ответ 54 кв. ед.