Найти общее решение дифференциальных уравнений !
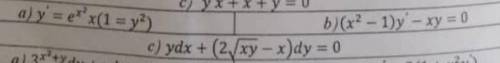
Другие вопросы по теме Алгебра
Популярные вопросы
- Шнитке это (не векипедия) кратко...
1 - Какого происхождения озёра. 30 1)ньяса 2)виктория 3)чад 4)альберт...
3 - Как распространяются радиоволны различных длин? (коротко)...
1 - Выберите беспозвоночное,у которого внутренние органыи ткани погружены в кровь.а)...
1 - Урезультаті біологічного аналізу в молекулі ірнк людини виявлено нуклеотидів: 440...
1 - 1из 1 прочитайте текст. золотой дождь всё лето листья подставляли солнцу свои ладошки...
3 - Просклоняите порядковые числительные (15,48,200)...
3 - Низкий человек (его поступки и тд) -что это метафора ,фразеологизм и тд? как объяснить...
1 - Речовина має масовий склад: c-37,5%,o-50%,h-12,5. визначте молекулярну формулу...
1 - Слагаемое _, 8, , слагаемое 10, _, _, сумма 18,17,16,15,14,13,12...
3
a)
сразу сократим 1/2
общее решение
б)
общее решение
в)
общее решение