Найти наименьшее целое число удовлетворяющее неравенству (5-√26)x< 51-10√26

Ответы

ADRELE 08.10.2020 22:04

$(5-\sqrt{26})x$

Разделим левую и правую часть на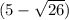 $(5-\sqrt{26})$ , сменив знак неравенства на противоположный, так как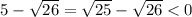 $5-\sqrt{26}=\sqrt{25}-\sqrt{26}$

$x\dfrac{51-10\sqrt{26} }{5-\sqrt{26}}$

Преобразуем дробь:

$\dfrac{51-10\sqrt{26} }{5-\sqrt{26}}=\dfrac{(51-10\sqrt{26})(5+\sqrt{26}) }{(5-\sqrt{26})(5+\sqrt{26})}=\\\=\dfrac{255+51\sqrt{26}-50\sqrt{26}-260 }{25-26}= \dfrac{\sqrt{26}-5 }{-1}=5-\sqrt{26}$

Тогда решение неравенства перепишется в виде:

$x5-\sqrt{26}$

Оценим значение:

$5=\sqrt{25}$

Таким образом, наименьшее целое число, удовлетворяющее неравенству - это число 0.

ответ: 0

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

p1ayer1337 08.07.2019 15:30

Как найти координаты точек пересечения графика с осями координат графика функции биквадратного уравнения: y=x4-20x2+100...

Artemmundryl 27.08.2019 21:40

Одно из чисел 4/7,6/7,8/7,13/7отмечены на прямой точкой 0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1...

avritsevich0116 27.08.2019 21:40

20 , пож-та! вычислить производную: y=1/4*(2x-1)^2...

sashaopalko123 27.08.2019 21:40

Решить логарифм log√2 по основанию 1/4...

arina68668 27.08.2019 21:40

Могут ли события с и d быть такими что р(c)=0.6, р(d)=0.7 и р(с∩d)=0.1...

академег228 09.11.2020 20:38

2 m• So=16 pd214c13 p239928c...

fraumiss93 09.11.2020 20:42

17. Дан треугольник с вершинами A (1; 1), B (5; 1) и C (3; 4). Найдите координаты точки, симметричной вершине B относительно начала координат этого треугольника. A) (-1; 5) B) (1;...

Анц 01.06.2021 17:53

Размеры бассейна: диаметр 366 см, высота 133 см, воды в бассейне каркасном 12тон, но в бассейне есть маленькая дырка, сколько уйдет воды за три месяца ...

NASTIAMURKA 01.06.2021 17:55

Решите неравенства Cos x корень 3:2 Sin 2x - корень 2:2 Cos 2 x корень 2:2...

dimanchik0108 01.06.2021 17:55

Нужно объяснение решения таких примеров...

Найти наименьшее целое число удовлетворяющее неравенству (5-√26)x< 51-10√26

Популярные вопросы