Найти интервал монотонности и точки экстремума y= 4x/4+x^2
Другие вопросы по теме Алгебра
Популярные вопросы
- Что значит фразеолагизм прокрутство ложе ?...
3 - Люди, мне нужно на ! мини-сочинение (чтобы мне не было стыдно его читать)...
2 - Даем полезные советы. семиклассник антон привык громко разговаривать и размахивать...
3 - Обозначают ли буквы ь , ь какие либо звуки ?...
2 - Подготовленный словарный диктант. страна,земля,сосна,гряда,тропа,звезда,вестна,...
3 - Яке число є найменшим спільним кратним чисел 24 і 18(будь ласка повна відповідь)...
1 - Три (икс минус игрек скобку закрываем = 60...
3 - Найти сторону квадрата если его периметр 84 см...
3 - Проект мое имя для ученицы первого класса на имя юлия, как сделать....
3 - Почему в слове лопата 6 звуков и 6 букв...
2
y'=4((4+x^2)-x*2x)/(4+x^2)^2=4(4-x^2)/(x^2+4)^2
(x^2+4)^2>0
4-x^2>0 x^2<4 (-2;2) y'>0 функция возрастает
x<-2 U x>2 функция убвает
у(-2) минимум
у(2) максимум
у(-2)=-1
у(2)=1
\ищчув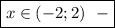 интервал возрастания
интервал возрастания