Найти границу числовой последовательности, n Є R
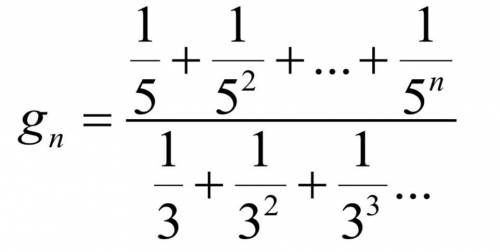
Другие вопросы по теме Алгебра
Популярные вопросы
- Как посчитать интеграл от 1 до е(в числителе( ln^2)х ,а знаменателе х) распишите...
2 - Вместо точек for или since i`ve known were at school i`ve wore contact years we`ve...
3 - Какое наименьшее значение может принимать выражение 9a^2+37-42a? а)12 б)-12 в)7...
2 - Человеку, сахарным диабетом, необходимо регулярно...
3 - (6 класс) : что вы будите делать если станет холодно или жарко, используйте рамочку...
1 - Две вершины квадрата ,расположенного на диогонали другого квадрата со стороной...
1 - Унас в блудовом болоте эти холмы песчаные покрытые высоким бором называют боринами...
3 - Вычислите относительные молекулярные массы соединений: а) hcn, б) hno3, в) нсlо4...
2 - Нужно написать очинение на тему: как мне статьчемпионом школы по плавнию или в...
1 - Что общего у мхов у папоротников и цветков...
3
ответ: lim gₙ=1/2.
Объяснение:
В числителе находится бесконечная убывающая геометрическая прогрессия с первым членом b1=1/5 и знаменателем q=1/5. Её предел S1 при n⇒∞ равен S1=b1/(1-q)=1/5/(4/5)=1/4. В знаменателе находится бесконечная убывающая геометрическая прогрессия с первым членом b1=1/3 и знаменателем q=1/3. Её предел S2 при n⇒∞ равен S2=b1/(1-q)=1/3/(2/3)=1/2. Отсюда lim gₙ=1/4/(1/2)=1/2.