Найти 5 член геометрической прогрессии !!

Объяснение:

1).

b1 = -20, b2 = 2.

Тогда знаменатель геометрической прогрессии равен: q = b2 / b1 = 2 / (-20) = 0,1.

Тогда b6= b1 * q(6-1) = -20 * (0,1)5 = 0,0002.

bn = b1 * q(n-1)

bn = -20 * 0,1(n-1)/

ответ: -0,0002; -20 * 0,1^(n-1)

0,002

Объяснение:

Найдём значение знаменателя данной геометрической прогрессии.

q = 2 : (- 20) = - 0,1.

Запишем формулу n-ного члена прогрессии.

= ·

При q = - 0,1 формула имеет вид = ·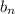  

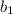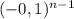
Найдём пятый член прогрессии.

= (- 20) · = (- 20) · = 20 · = 20 · 0,0001 = 0,002.