Найдите значения a и b при которых данное тождество верное : 3x^5 - x^4+x^3-4x+1=(x^2 -1)(3x^3 +Ax^2 +Bx) (с решением)
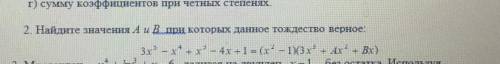
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать сочинение на казахском на тему біздің заманның данагөйлері...
2 - Водинаковых пакетах 24кг картофеля.сколько кг картофеля в 5 таких пакетах?...
3 - Найти площадь прямоугольника, стороны которого равны корень 3+1 и корень...
2 - Қола дәуіріндегі ыдыс жасаудың ең бір өрістеген түрі...
3 - Что нужно сделать, что бы определить, к какому склонению относится существительное?...
1 - Скласть и написать сказку про осень природа 2 клас...
3 - 7класс почему надо читать песню про царя ивана васильевича, молодого...
1 - 9класс 16/(х^2 -2х) - 11/х^2-2х = 9/ х^2-2х+1...
1 - Округлите число 1,35769231 до тысячных....
2 - Функции и значение органинечских и неорганических клеток , 6 класс...
1
Начнем с раскрытия скобок на правой стороне:
(x^2 - 1)(3x^3 + Ax^2 + Bx) = 3x^5 + Ax^4 + Bx^3 + 3x^3 - Ax^2 - Bx - 3x^3 - Ax^2 - Bx = 3x^5 + (A - 1)x^4 + (B - A)x^3 - 2Ax^2 - 2Bx
Теперь мы можем сравнить коэффициенты при одинаковых степенях x с коэффициентами на левой стороне.
Сравнивая коэффициенты при x^5, у нас есть:
3 = 0 (так как у нас нет члена с x^5 на левой стороне)
Это означает, что a и b не имеют значения при x^5.
Сравнивая коэффициенты при x^4, у нас есть:
-1 = A - 1
Это означает, что A = 0.
Сравнивая коэффициенты при x^3, у нас есть:
1 = B - A
Подставляя значение A = 0, мы получаем:
1 = B
Сравнивая коэффициенты при x^2, у нас есть:
0 = -2A
Это означает, что A = 0.
Сравнивая коэффициенты при x, у нас есть:
-4 = -2B
Разделим обе части на -2:
2 = B
Итак, значения a и b, которые делают данное тождество верным, равны:
a = 0
b = 2