Алгебра: Найдите значение выражения a/2-3a, если a=5хееелп

Найдите значение выражения a/2-3a, если a=5
хееелп

Ответы

vladimirnishta1 24.05.2021 06:00

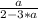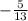Если значение выражения равно $\frac{a}{2-3*a}$ , то ответ будет равен $-\frac{5}{13}$ .

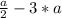Если значение выражения равно $\frac{a}{2}-3*a$ , то ответ будет равен -12,5 .

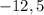Объяснение:

Нам дано выражение: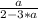 $\frac{a}{2-3*a}$ , и известно значение неизвестной переменной a=5 .

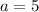В самом выражении упрощать нечего, поэтому нам нужно всего лишь подставить значение переменной в само выражение:

$\frac{a}{2-3*a}=\frac{5}{2-3*5}=\frac{5}{2-15}=\frac{5}{-13}=-\frac{5}{13}$ .

Сделали перемножение двух чисел в знаменателе, далее из 2 вычли полученное произведение этих чисел, получили отрицательное число в знаменателе. Имеем право вынести его за знак получившейся дроби. В итоге получили ответ.

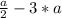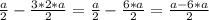
Или если значение выражения имеет вид: $\frac{a}{2}-3*a$ , то тогда приводим к общему знаменателю числа, домножив 3*a на 2: $\frac{a}{2}-\frac{3*2*a}{2}=\frac{a}{2}-\frac{6*a}{2}=\frac{a-6*a}{2}$

Теперь подставляем значение нашей переменной:

$\frac{a-6*a}{2}=\frac{5-6*5}{2}=\frac{5-30}{2}=\frac{-25}{2}=-\frac{25}{2}=-12\frac{1}{2}=-12\frac{1*5}{2*5}=-12\frac{5}{10}=-12,5$ .

В данном случае перемножили два числа в числителе, далее вычли из 5 полученное произведение, получили отрицательное число в числителе, вынесли знак "-" за дробь, и преобразовали дробь в десятичную.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра