Найдите все целые значения p,при которых уоавнение x²-px-10=0 имеет целые корни
Другие вопросы по теме Алгебра
Популярные вопросы
- Известно,что числа n-8 и n+9 являются квадратами натуральных чисел. найти...
1 - Разобрать предложения по членам предложения 1. дорожка эта скоро превратилась...
1 - Составь множество двухзначных чисел в записе которых используются лишь...
2 - Задумали число збільшили вдвічі , відняли 15 і поділили на 3 . отримали...
2 - Запишите на языке правило сложения обыкновенных дробей чтобы сложить дроби...
2 - Решить систему уравнений: a(b−c+1) = b^2−bc+c, b(c−a+1) = c^2−ca+a, c(a−b+1)...
1 - Попугай и медвежонок,чиж с и с с и разбежались кто куда,-ка их сюда! (как...
3 - 1. в кружок (не)добрали нескольких учеников. 2. рис в пирожках был недоварен...
1 - 4. чему равны заряд ядра и число электронов в атомах следующих элементов:...
1 - Слова з префіксом пре при прі 3 речення з словами з префіксом пре при прі...
2
Так как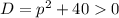 , то по теореме Виета
, то по теореме Виета
И решим уравнение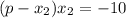 в целых числах.
в целых числах.
Делители числа 10: 1, 2, 5, 10.
ответ: ± 3; ± 9.