Найдите все а, при которых есть хотя бы 1 решение

Question

Алгебра: Найдите все а, при которых есть хотя бы 1 решение

пупсик145 · Answer

Рассмотрим функцию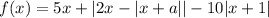 f(x)=5x+|2x-|x+a||-10|x+1| . Её график представляет собой некоторую бесконечную ломаную, состоящую из частей прямых с разным углом наклона.

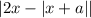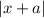Даже если модули |2x-|x+a|| и |x+a| раскроются так, чтобы перед иксами везде был плюс (получится 8x), то угол наклона всё равно будет зависеть от того, как раскроется модуль 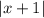|x+1| , то есть при x ≥ -1 8x-10x = -2x — функция убывает; при x < -1 8x+10x = 18x — функция возрастает. Так как больше 8x мы получить не можем, x = -1 — точка максимума этой функции. Значит, это уравнение (f(x) = 0) имеет хотя бы одно решение, если

$\displaystyle f(-1)\geq 0\\-5+|-2-|a-1||-10|1-1|\geq 0\\|2+|a-1||\geq 5\\\left [ {{2+|a-1|\geq 5} \atop {2+|a-1|\leq -5~(-)}} \right. \\|a-1|\geq 3\\\left [ {{a-1\geq 3} \atop {a-1\leq -3}} \right.\\\left [ {{a\geq 4} \atop {a\leq -2}} \right.$

ответ: $(-\infty;-2]\cup[4;+\infty)$

Найдите все а, при которых есть хотя бы 1 решение

Популярные вопросы