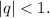Найдите сумму ряда
sin π/3+ sin² π/3 +sin³ π/3+...+sin^n π/3+...
Другие вопросы по теме Алгебра
Популярные вопросы
- За три дня рабочие уложили 1 329 м 2 газона сколько квадратный метрв они уложат...
3 - Найдите дробь от суммы 1 целая 5/7 от 3/20+1/10...
3 - Cкаким ускорением будет двигаться c каким ускорением будет двигаться тело массой...
2 - Симптомом инфекционного заболевания может служить повышение содержания в крови...
1 - Зная строение галогенов, объясните, почему у фтора самая высокая окислительная...
2 - Папа мама. сын поехали навестить бабушку.общее. расстояние которое им надо проехать1300км...
1 - Что изменилось когда к власти пришел николаи 2?...
2 - Вспомните имена существительные на тему школа из орфографического словаря. запишите,распределяя...
2 - Убуратино в кармане лежит 8 рублей тремя монетами. одна из них не двухрублевая...
2 - Вкорзине было неизвестное колличество яблок.сначало из неё взяли 12 яблок а...
1
Бесконечно убывающая геометрическая прогрессия с первым членом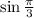 и знаменателем
и знаменателем 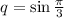 . ВАЖНО: геометрическая прогрессия бесконечно убывающая тогда, когда
. ВАЖНО: геометрическая прогрессия бесконечно убывающая тогда, когда