с алгеброй!
Делится ли 7^2017 + 4 ^2018 + 3 ^ 2019 на 10? Полностью обоснуйте свой ответ.

Число делится на 10 только в том случае, если оно оканчивается цифрой 0.

Посмотрим, какой цифрой оканчивается каждое слагаемое.

1) число 7 в разных степенях оканчивается разными цифрами. Попробуем установить закономерность.

Т.е. последние цифры записи степеней семерки чередуются так: 7 - 9 - 3 - 1 и по кругу.

Т.к.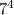 оканчивается цифрой 1, то 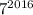также оканчивается цифрой 1. Тогда число 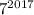оканчивается цифрой 7.

2) Для степеней четверки закономерность проще - 4 - 6 и по кругу:

Поскольку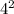 оканчивается цифрой 6, то  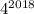 также оканчивается цифрой 6.

3) Закономерность для степеней тройки - 3 - 9 - 7 - 1 и по кругу:

Т.к.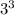 оканчивается цифрой 7, то 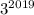также оканчивается цифрой 7.

В итоге слагаемые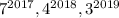 оканчиваются цифрами 7, 6 и 7 соответственно. Если их сложить, то в разрядке единиц класса единиц получим 0. Т.е. число 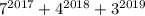оканчивается цифрой 0 - следовательно, оно таки делится на 10.

ОТВЕТ: да.