Найдите сумму членов арифметической прогрессии с 6 по 31 включительно, если первый член равен 7 и разность равна 3.
Ответы
По условию a1=7, d=3. Тогда 6 член а6= а1+5*d=7+5*3=22, и 31 член a31=a1+30*d=7+30*3=97. В общем случае сумма n первых членов равна 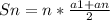 . Сумма первых 6 членов равна S6=0,5*(7+22)*6=87. Сумма первых 31 членов равна S31=0,5*31*(7+97)=1612. Искомая сумма равна S=S31-S6=1612-87=1525.
. Сумма первых 6 членов равна S6=0,5*(7+22)*6=87. Сумма первых 31 членов равна S31=0,5*31*(7+97)=1612. Искомая сумма равна S=S31-S6=1612-87=1525.
ПОКАЗАТЬ ОТВЕТЫ
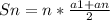 . Сумма первых 6 членов равна S6=0,5*(7+22)*6=87. Сумма первых 31 членов равна S31=0,5*31*(7+97)=1612. Искомая сумма равна S=S31-S6=1612-87=1525.
. Сумма первых 6 членов равна S6=0,5*(7+22)*6=87. Сумма первых 31 членов равна S31=0,5*31*(7+97)=1612. Искомая сумма равна S=S31-S6=1612-87=1525.
Другие вопросы по теме Алгебра
Популярные вопросы
- с русским!! ( ) Выделите грамматические основы в (3) предложении и укажите...
1 - Этот композитор говорил «Моя скрипка никогда не выходит из дома». Как...
1 - 1. а) По рисункам 1-3 определите открытия, изменившие мир - Б) Опишите...
3 - 1. Прочитайте текст. Найдите ключевые слова и определите тему. Как вы...
2 - Choose one variant 1.British people keep their … a) kingdom b)traditions...
3 - Текст Reading (the second term) My name is Tom Austin. I live in a small...
3 - Математика 2 сынып қосудың терімділік және көбеитудің орын ауыстырымдылық...
2 - Порівняйте владу імператора династії Цин, сьогуна Японії з владою европейских...
3 - .Укажите, о ком идет речь. Правление его было неизбежным злом — страна...
1 - Найдите на сколько масса 3 кубических метров железа будет больше чем...
3