1. Алгебра
  2. Найдите среднее арифметическое(

Найдите среднее арифметическое( в градусах) корней уравнения cos³x+sin³x =1 на промежутке [-2п; 2п]

Apsalikovat Apsalikovat    3   17.08.2019 11:56    2

Ответы
irna200 irna200  05.10.2020 00:40

\sin^3x+\cos ^3x=1\\ \\ (\sin x+\cos x)(\sin^2x-\sin x\cos x+\cos^2x)=1\\ \\ (\sin x+\cos x)(1-\sin x\cos x)=1

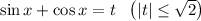Пусть \sin x+\cos x=t~~\left(|t|\leq\sqrt{2}\right), возведя обе части равенства, получим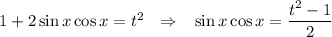 1+2\sin x\cos x=t^2~~\Rightarrow~~ \sin x\cos x=\dfrac{t^2-1}{2}

t\left(1-\dfrac{t^2-1}{2}\right)=1~~~|\cdot 2\\ \\ 2t-t^3+t=2\\ \\ t^3-3t+2=0\\ \\ t^3-t^2+t^2-t-2t+2=0\\ \\ t^2(t-1)+t(t-1)-2(t-1)=0\\ \\ (t-1)(t^2+t-2)=0 \\ \\ (t-1)^2(t+2)=0\\ t_1=1\\ t_2=-2

Второй корень t = -2 не удовлетворяет условию |t| ≤ √2.

\sin x+\cos x=1\\ \\ \sqrt{2}\sin \left(x+\frac{\pi}{4}\right)=1\\ \\ \sin \left(x+\frac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\\ \\ x=(-1)^{k}\cdot \dfrac{\pi}{4}+\dfrac{\pi}{4}+\pi k,k \in \mathbb{Z}

Отбор корней

n = 0; x = π/2n = 1;  x = πn = -1;  x = -πn = -2; x = -3π/2

Среднее арифметическое корней:

\dfrac{\pi/2+\pi -\pi-3\pi/2}{4}=-\dfrac{\pi}{4} или это -45°

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
heartanime heartanime  31.08.2019 14:00
Решите систему уравнений {2у=-х+13 {х+у=11...
Лизок070707 Лизок070707  31.08.2019 14:00
7cos^2x-cosx-8=0 и область определения от -7пи/2 до -3пи/2...
nika12052006 nika12052006  31.08.2019 14:00
Найди координаты вершины параболы y=0,1x2−7x+15...
smoboine smoboine  31.08.2019 14:00
Найди сумму первых 4 членов прогрессии, если b1=−0,8 и знаменатель равен −1...
cemikhadam cemikhadam  31.08.2019 14:00
1)функция задана формулой у=-5x+10 определите а)чему равно значение y при x=2,5 б)при каком значении x значение у равно 5 в)подходит ли график функции через точку b(3; 5) 2) постройте...
Клевая401 Клевая401  31.08.2019 14:00
(x-2)^4+(x-2)^2-2=0 .решите уравнение...
natsvin2017 natsvin2017  23.04.2020 17:37
Бак объёмом 425 м^3 был наполнен водой из двух кранов, причём первый кран был открыт на 5 ч дольше второго. Если бы первый кран был открыт столько времени, сколько на самом деле...
769429 769429  23.04.2020 17:37
Знайти суму : 1)1-2+4-...+256 2) 1/4+1/8+1/16+...+1/512...
кама148 кама148  23.04.2020 17:37
У выражение (3a + 2)(9a2 – 6a + 4) и найдите его значение при a = 1\3...
marychka0783 marychka0783  23.04.2020 17:37
Знайдіть значення функції у=8х-3,якщо значення аргументу дорівнює -1​...

Популярные вопросы