Найдите производную функции
Другие вопросы по теме Алгебра
Популярные вопросы
- )преобразуйте выражение в одночлен стандартного вида : 1) -3а²b⁴ˣ3а² ˣb⁵...
1 - Найдите высоту правильной треугольной пирамиды если сторона основания...
2 - Почему реформацию называли королевской ? кто в выступал в её поддержку...
1 - Начерти два отрезка.длина первого отрезка 4 см. второй отрезок в 2 раза...
2 - Аккорды в ми диес мажоре. 1- т53,s64,t53,t6,s53,t64,d53,t53 ....
3 - Краздвижной расчёт расчёт чатай основе юрте из 6 секций привязывать 72...
1 - Вящике 400 деталей вероятность брака 0.02%- сколько бракованых в ящике?...
3 - Саодат задумал число.вначале он умножил его на 15,и это же число задумал...
2 - Эссе по на тему идеи просветителей 18 века...
1 - Сочинение рассуждение на тему может ли разбойник быть благородным из романа...
3
1)f'(x)=2x+4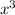 -9
-9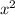
f'(0)=0
2)f'(x)=
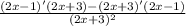 =
=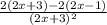 =
=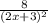
f'(2)=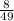
3)f'(x)=(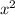 )'
)'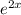 +(
+(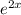 )'
)'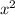 =2x
=2x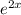 +2
+2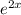
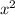 =
=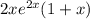
4)f'(x)=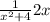
5)f'(x)=4*2cosx(-sinx)=-4sin(2x)
6)f'(x)=
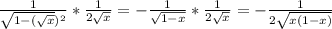
f'(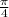 =
=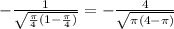
1. f'(x)=(х²+х⁴-3х³+2)'=2x+4x³-6x f'(0)=0
2. f'(x)=(2*(2x+3)-2*(2x-1))/(2x+3)²=8/(2x+3)²; f'(2)=8/(7)²=7/49
3. f'(x)=2х*е²ˣ+х²*2е²ˣ=2хе²ˣ*(1+х)
4. f'(x)=2х/(х²+4)
5. f'(x)=-8cosxsinx=-4sin2x
6. f'(x)=(-1/(√(1-x))*(1/2√x); f'(π/4)=(-1/√1-π/4)*(1/2*((√π)/2)))=
(-1/√1-π/4)*(1/2*((√π)/2)))=-√π√(4-π)/π√π=-√(4-π)/π.