Найдите площадь фигуры , ограниченной прямой x=b, осью OX и графиком функции y=f (x) , если:
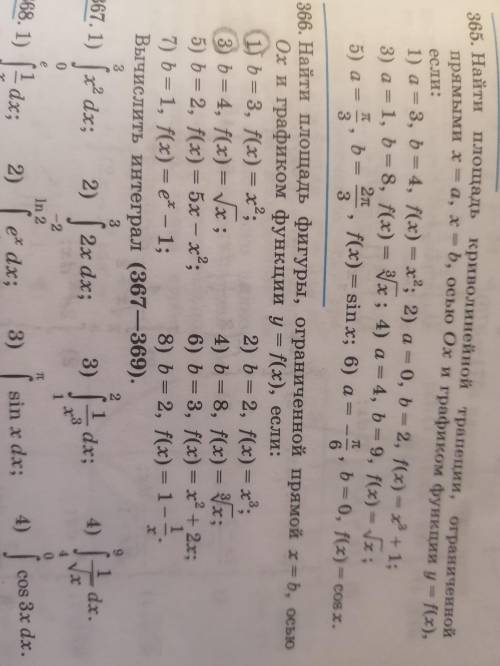
Другие вопросы по теме Алгебра
Популярные вопросы
- Вставить am,is,are.i am happy,2)this__my brother tom.3) how ? i old.4)where...
3 - су тіршілікке көзі эссе жазу. хотя бы 10 предложений с переводом....
1 - Напишите программу,чтобы можно было определить,какое из двух чисел...
3 - Однажды мама ушла .что успокоило малыша?...
1 - Сочинение моя любимая книга алиса на планете загадок...
3 - Собственная скорость лодки 8,6км\ч скорость течения реки 2,5км\ч ....
1 - Что такое пестушка, потешка, колыбель, закличка, приговорка, прибаутка,...
2 - Расфасовывали 36 кг крупы поповну в 12 пакетов . сколько пакетов потребуется...
3 - Составить 3 на проценты с решением нужно 6 класс 30...
1 - Сочленение по укр лит придумать название моя первая книга...
3
Для начала давайте разберемся с условием задачи. У нас есть фигура, ограниченная прямой x=b, осью OX и графиком функции y=f(x). Наша задача состоит в нахождении площади этой фигуры.
Для решения этой задачи мы можем использовать интеграл. Интеграл - это математическая операция, позволяющая найти площадь под кривой на заданном интервале.
Давайте разобьем наш интервал [0, b] на бесконечно малые части, каждую из которых мы обозначим как dx. Теперь мы можем записать площадь фигуры как интеграл от 0 до b функции f(x) по переменной x. Обозначим это как S:
S = ∫[0,b] f(x) dx
Теперь нам нужно вычислить этот интеграл. Для этого нам понадобится знание функции f(x). Предположим, что у нас есть квадратная функция f(x) = ax^2 + bx + c, где a, b и c - это некоторые константы.
Теперь мы можем заменить f(x) в нашем интеграле:
S = ∫[0,b] (ax^2 + bx + c) dx
Для вычисления этого интеграла мы можем использовать правила интегрирования. В нашем случае, мы должны интегрировать каждое слагаемое отдельно.
∫ ax^2 dx = (a/3) * x^3
∫ bx dx = (b/2) * x^2
∫ c dx = c * x
Теперь мы можем получить окончательное выражение для площади S:
S = (a/3) * x^3 + (b/2) * x^2 + c * x
Теперь давайте применим верхний и нижний пределы к нашему интегралу:
S = [(a/3) * b^3 + (b/2) * b^2 + c * b] - [(a/3) * 0^3 + (b/2) * 0^2 + c * 0]
= [(a/3) * b^3 + (b/2) * b^2 + c * b] - 0
= (a/3) * b^3 + (b/2) * b^2 + c * b
Таким образом, мы получили выражение для площади фигуры, ограниченной прямой x=b, осью OX и графиком функции y=f(x):
S = (a/3) * b^3 + (b/2) * b^2 + c * b
Мы предположили, что функция f(x) является квадратной функцией, однако это решение может быть обобщено для других функций. В таком случае, вычисление площади будет зависеть от конкретной формы функции f(x) и может потребовать использования других методов.
Я надеюсь, что это решение было понятным и полезным для вас. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их. Желаю вам успехов в изучении математики!