1. Алгебра
  2. Найдите: первый член и знаменатель

Найдите: первый член и знаменатель прогрессии, если b3=4, b5=16.
, используя формулу n-ного члена прогрессии. ❤️ много !

levkim levkim    2   04.12.2019 16:29    0

Ответы
alena667 alena667  11.09.2020 15:00

Найдём 4-й член. Он равен среднему геометрическому соседних членов (возможно, взятому и со знаком минус, если прогрессия знакочередующаяся):

b_4^2=4 \cdot 16=64\\b_4=\pm \sqrt{64}= \pm 8

Рассмотрим два случая.

Первый случай

b_4=8. Тогда знаменатель равен q=b_5/b_4=16/8=2. Первый член найдём из формулы 3-го члена:

b_3=b_1q^2=4\\b_1 \cdot 2^2=4\\b_1=1

Второй случай

b_4=-8\\q=b_5/b_4=16/(-8)=-2\\b_1q^2=4\\b_1 \cdot (-2)^2=4\\b_1 \cdot 4=4\\b_1=1

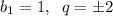
ответ: b_1=1, \; \; q= \pm 2

ПОКАЗАТЬ ОТВЕТЫ
lianochkaya14 lianochkaya14  11.09.2020 15:00

Объяснение:

-----------------------------


Найдите: первый член и знаменатель прогрессии, если b3=4, b5=16. , используя формулу n-ного члена п
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
aytanpashaeva aytanpashaeva  28.02.2019 18:20
Розвяжите неравенство: 2-7x 0; 6(y-1,5)-3,4 4y-2,4...
сакура23 сакура23  28.02.2019 18:20
Мастер и его ученик вместе могут изготовить за 1 час 17 деталей .до обеда мастер проработал 4 часа, а ученик 2 часа. вместе они изготовили 54 детали. сколько деталей изготовил...
Eva345678 Eva345678  28.02.2019 18:20
Из двух пунктов реки навстречу друг другу движутся две моторные лодка собственные скорости которых равны .довстречи лодки идущая по течению, шла 1,1 ч, а лодка , идущая против...
nastponomarenk nastponomarenk  28.02.2019 18:20
1. найдите все корни уравнения(х-1999)=-1999 это все в модуле! ) 2. девочки составляют 3/5 нашего класса, 1/7 их числа – отличницы. сколько учащихся в нашем классе? 3. в спортинвой...
Gibertblite Gibertblite  28.02.2019 18:20
.(1) применяя теорему безу найдите остаток от деления многочлена p(x) на двухчлен q(x) в) p(x)= x³+x²-x+8,q(x)=x+ 2) выполните деления p(x): q(x) если: а) p(x)= x⁵-x³+x, q(x)=x²-...
Эноа Эноа  28.02.2019 18:20
Выражение и найдите его значение: 6*(3х+5y)+7x-5y при х+y=3...
artem0941 artem0941  28.02.2019 18:10
Сумма трех чисел равна 496. второе число составляет 8/15(восемь пятнадцатых) от первого, а первое число меньше третьего в 2.3/5(две целых. три пятых) раза. найдите каждое...
Valentinka14485 Valentinka14485  28.02.2019 18:10
Знайдіть множину значень функції y= -2 x^{2} +4x-10...
patya6346 patya6346  28.02.2019 18:10
Решить системы с формул крамера 1) 2x + 3y = 13 5x - y = 7 2) 5x + 3y + 3z = 48 2x + 6y - 3z = 18 8x - 3y + 2z = 21...
shchevelevn shchevelevn  28.02.2019 18:10
1) выполнить действия a) (x+y)⁻⁵ · (x+y)² (x+y)⁻² · (x+y)⁻¹ b) ²√x ÷ x⁻⅔ 2) выражение m(в степени 3/2) - n (в степени 3/2) √m - √n...

Популярные вопросы