Найдите область определения функции
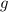y = \sqrt{3 - 5x - 2 {x}^{2} } )
akimhikp01b5f
1
14.12.2019 00:26
0
Другие вопросы по теме Алгебра
ЕлизабетклассD
30.06.2019 07:30
Savelijbih
30.06.2019 07:30
BLACK2IVAN
30.06.2019 07:30
Auyrey03
30.06.2019 07:30
sofavorobyova17
30.06.2019 07:30
AnyMay00853
30.06.2019 07:30
EeeeeeeROOOCK
30.06.2019 07:30
Loooooper
14.09.2019 21:50
mara1427
14.09.2019 21:50
kirill4389
14.09.2019 21:50
Популярные вопросы
- А) выразить в дециметрах: 1/2м, 1/10м. б) выразить в сантиметрах: 1/5м;...
1 - Существовали 13 колоний в америке в 1773 году....
2 - Всостав боярской думы в 17 веке входили . . а)стряпчие б)воеводы г)окольничие...
1 - Подготовьте ответ о диффузии по плану ответа о явлении. заранее !...
3 - Какие ошибки допустил нерадивый ученик в следующих устойчивых сочетаниях...
2 - Сравните значения выражений 112/64 и 9/4 72/144 и 36/108 81/45 и 56/48...
2 - Составьте и реши ее столовых ложек-10, чайных ложек-7, на сколько больше...
3 - Расставь скобки так что бы значение выражения было верным 26+4*5-2=90...
3 - Как составить 2 предложения из слов армия,комедия,линия,планетарий,лекция,...
3 - Выражение: 1.) (a+2)(a-5)-3a(1-2a) -7)(3a-+1)(2a-4)...
3
Объяснение:
Решим уравнение:
Тогда по методу интервалов:
----- + ---- -3 ------ - -------- 1/2 -------- + ------->x
Тогда ответ:
3-5х-2х²≥0
-3+5х+2х²≤0
х=(-5±√(25+24))/4=(-5±7))/4; х=-3; х=1/2;
2*(х+3)(х-0.5)≤0
Решаем методом интервалов.
-30.5
+ - +
х∈(-3;0.5)