1. Алгебра
  2. Найдите наименьшее значение

Найдите наименьшее значение функции у=14sin+(72/pi)*x+26 на отрезке [-5pi/6; 0] (решение через производную)

Metyakarimi Metyakarimi    1   20.06.2019 15:10    6

Ответы
Angeloc2567 Angeloc2567  16.07.2020 14:21

1. Производная функции:

y'=\left(14\sin x+\frac{72x}{\pi}+26\right)'=14\cos x+\frac{72}{\pi}


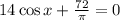
2. y' = 0;  14\cos x+\frac{72}{\pi}=0\\

\cos x=-\frac{36}{7\pi}

Это уравнение решений не имеет, т.к. косинус изменяется от -1 до 1.


3. Найдем наименьшее значение функции на концах отрезка.

y\left(-\frac{5\pi}{6}\right)=14\sin \left(-\frac{5\pi}{6}\right)-\frac{72}{\pi}\cdot\frac{5\pi}{6}+26=14\cdot (-0.5)-60+26=-41 - min

y(0)=14\sin 0+\frac{72}{\pi}\cdot0+26=26



ответ: \displaystyle \min_\big{\left[-\frac{5\pi}{6};0\right]}y(x)=y\left(-\frac{5\pi}{6}\right)=-41

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
okhotnikoffzhep08lws okhotnikoffzhep08lws  04.03.2020 00:09
Из пунктов а и в одновременно навстречу друг другу вышли два пешехода. скорость первого на 2км/ч меньше чем скорость второго поэтому он прибыл в пункт в на 1 час раньше чем второй...
сас001 сас001  04.03.2020 00:14
Из колоды на 36 карт берут 4.Найти вероятность того, что среди них есть ровно 2 туза...
Сонька10Монька Сонька10Монька  04.03.2020 00:16
Работая вместе два маляра смогут закончить работу за 6 дней. Сколько времени понадобиться для выполнения всего задания каждому из них если второй работая в отдельности закончил...
Индира347 Индира347  04.03.2020 00:28
Учусь на прикладной математике. Почему даже за мой во учительница на меня наорала. Почему ответ квадратного корня ≥ 0 и всегда положительный. Она говорит что √9 только 3, без +-3...
denisstar756 denisstar756  04.03.2020 00:34
При якому значенні х значення виразу 0,5х-0,5(1,2х-0,8) дорівнює -0,5 ​...
gurulezz1257 gurulezz1257  04.09.2019 09:53
Решить 1) 2,4² -2 •2,4 •1,4+ 1,4²= 2⁷•2² = (2³)³ 2) 14⁵ —- = 7⁵ 3) 0,75² - 6,74² = 4) выражение. 1) -2 (3a- b) + 6a = 2) (m- 2n)² + 4mh = 3) (a+8b) (-a+8b) =...
mashashhukina mashashhukina  04.09.2019 09:53
Решить 1) 2,4² -2 •2,4 •1,4+ 1,4²= 2⁷•2² = (2³)³ 2) 14⁵ —- = 7⁵ 3) 0,75² - 6,74² = 4) выражение. 1) -2 (3a- b) + 6a = 2) (m- 2n)² + 4mh = 3) (a+8b) (-a+8b) =...
AidarSharafutdinov AidarSharafutdinov  04.09.2019 10:00
1)найдите периметр треугольника со сторонами 4,26см , 5,09 см и 6,8см 2)ширина прямоугольного параллелепипеда 8см, длина 6 см, а высота на 3 см больше ширины. найдите объем прямоугольного...
artemantonuc artemantonuc  04.09.2019 11:10
Перевести с на my sister is my father my mother is my father s my father is it me out is my brother my father is my mother s mother is out номер 2...
михаил303 михаил303  04.09.2019 10:12
Морковь выращенная фермером была продана за 3 дня в 1 день было продано 25 %моркови во 2 день 50% всей моркови а в 3 последнеей 150 кг сколько всего кг моркови выростил фермер...

Популярные вопросы