1. Алгебра
  2. Найдите наименьшее значение

Найдите наименьшее значение функции на отрезке [0; 3]
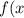f(x)=x^{3} -3x

nazarzadorozhny nazarzadorozhny    3   11.07.2019 16:06    1

Ответы
HelpMePlsIs HelpMePlsIs  06.08.2020 23:22

f'(x)=3x^2-3

Найдём нули производной:

3x^2-3=0\\x^2-1=0\\x=\pm 1

При x\in(-\infty;-1]\cup [1;+\infty) производная неотрицательна, значит, на данном промежутке функция возрастает.

При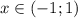 x\in (-1; 1) производная отрицательна, значит, на данном промежутке функция убывает.

Таким образом, точка минимума функции — x = 1. На отрезке [0; 3] функция принимает наименьшее значение именно в этой точке. Значит, наименьшее значение функции на заданном промежутке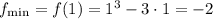 f_{\min}=f(1)=1^3-3\cdot 1=-2.

ответ: -2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
6lackk 6lackk  26.12.2019 10:54
Тригонометрических уравнений cosx=0,7 sinx=19 ctgx=47​...
korostin2004 korostin2004  26.12.2019 10:55
Вычислить значение производной в точке x=2 для функции y=x^5–1/2x. фото( 3)...
wazap100 wazap100  26.12.2019 10:58
Построить график функции y=-8/х найти с графика при каких значениях х y=4,значение y при х=2...
Darhanfan Darhanfan  26.12.2019 10:59
3и 4 , в 4 вместо точек умножение...
adel2006buko adel2006buko  26.12.2019 11:03
[tex] \sqrt[3]{128} + \sqrt{ \frac{1}{4} } [/tex]через photomatch не правильно, решить ​...
shmkvnst17 shmkvnst17  26.12.2019 11:07
Знайдіть довжину вектора a = 2 p − q , якщо | p | = 1 ; | q | = 2 ; ∠ ( p ; q ) = 60°...
kokoko29 kokoko29  26.12.2019 11:09
Школьный комитет,состоящий из 5 студентов, избирается из 8 мальчиков и 6 девочек. сколькими можно выбрать членов комитета?...
danadv danadv  26.12.2019 11:10
Производная сложная функция !...
Августина3008 Августина3008  26.12.2019 11:11
Подайте у вигляді степеня вираз (фото)...
LaMihaLa LaMihaLa  26.12.2019 11:11
На складе лежат три слитка меди. известно, что первый слиток весит 4 кг, а второй — 9 кг. содержание меди в первом слитке составляет 30, а во втором слитке — 20. если...

Популярные вопросы