1. Алгебра
  2. Найдите наибольшее целочисленное

Найдите наибольшее целочисленное решение неравенства f(x)-f ' (x)< 0, если f(x)=3x^2+18x+8.

Iraa26 Iraa26    3   10.06.2019 09:10    5

Ответы
Mary2304Cat Mary2304Cat  01.10.2020 23:41

f(x) = 3x²+18x+8;

f'(x) = 2·3x+18·1+0 = 6x+18.

f(x) - f'(x) < 0;

3x²+18x+8 - (6x+18) < 0;

3x²+18x-6x+8-18 < 0;

3x²+12x-10 < 0 (1)

Найдём х, при которых выражение равно нулю:

D = 12²-4·3·(-10) = 144+120 = 4·66

x =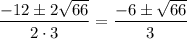 \dfrac{-12\pm 2\sqrt{66}}{2\cdot 3} =\dfrac{-6\pm \sqrt{66}}{3}

Решим неравенство (1) методом интервалом, смотри в приложении.

\dfrac{-6-\sqrt{66}}3

Необходимо найти наибольшее целое число, которое меньше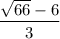 \dfrac{\sqrt{66}-6}3

\sqrt{64}

ответ: 0.


Найдите наибольшее целочисленное решение неравенства f(x)-f ' (x)< 0, если f(x)=3x^2+18x+8.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
2005kek 2005kek  25.07.2019 15:09
9и 10 номер, будьте так добры с решением за 30 !...
Braīŋľÿ Braīŋľÿ  25.07.2019 15:02
Объясните, как происходит умножение таких чисел как, например, [tex]6.7*10^{-11}*0.6*10^{3}[/tex], заранее : )...
ЭляВ1988 ЭляВ1988  25.07.2019 17:10
(3х-2)(3х+-1)во 2ой степени-(5х-1)(х+2)=23 но только с объеснением ну или нет...
ира1014 ира1014  25.07.2019 17:10
Выполните действия: 3(1+2xy)(1-2xy); (x^2+y^3)^2; (a+b)^2-(a-b)^2;...
Alica2653 Alica2653  25.07.2019 17:10
Из села в направлении города выехал мотоциклист со скоростью 80 км/ч. через 1,5 чиз города в село выехал велосипедист со скоростью 16 км/ч. сколько часов ехал до встречи каждый...
самая29 самая29  25.07.2019 17:10
Вычислить а)257²-143² б)73,6²-26,4² в)165²-65² ²-это квадрат если что...
kris0287 kris0287  25.07.2019 17:10
Кпереправе подошли 3 странника и 3 людоеда. оказалось,что на переправе имеется только одна лодка, которая может вместить лишь двух людей.странники боятся оставаться в меньшинстве...
ivchencov767 ivchencov767  05.07.2019 04:30
Сколько сможите хотя бы укажите знаки абциссы и ординаты точки числовой окружности найдите на числовой окружности точки с абцисой или ординатой удовлетворяющей заданному неравенству...
Faop Faop  05.07.2019 04:30
Найдите корень уравнения а)4(х+2)=8х+2 б) 0,4х+3=0,7(4х-6) найдите корень уравнения одна пятая 1х=20 _ 5 решите уравнение 7,5х-4=3,5+5х при каком значении y значение выражения...
anonim000002 anonim000002  05.07.2019 04:30
1.сколько корней имеет уравнение 2х=8? а.не имеет корней б.бесконечное множество в.два г.один. 2.решите уравнение -2х+4=-6 а.х=1 б.х=-1 в.х=5 г.х=-5 с решениями,вдруг ответ...

Популярные вопросы