Найдите множество решений неравенства ㏒²4 x-3㏒4 x+2≥0
Другие вопросы по теме Алгебра
Популярные вопросы
- На 8 г магний оксида подействовали сульфатной кислотой. Какая масса соли...
1 - У треугольника ABC и A1 B1 C1 угол А=углу А1 угол С=углу С1 АС=А1 С1=6...
3 - Образ бабушки в повести горького детство кратко...
3 - Капиллярные трубки с диаметрами 2мм и 1мм опущенны в воду. Определите...
3 - целые 17/18минус2целые7/12; 5целые 5/9минус2целые4/7...
3 - Мини-сообщение (1 лист А4) на тему: Их католические величества Изабелла...
2 - Выразить х через у у=3/х+1-2...
1 - по физике Частота колебаний электромагнитной волны 3ТГц. Определите длину...
2 - Один із зовнішніх кутів трикутника дорівнює 140°. Знайдіть внутрішні...
3 - Если бы памятник мог говорить.написать сочинение...
3
(0; 4] ∪[16; + ∞)
Объяснение:
Пусть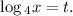 Тогда неравенство принимает вид :
Тогда неравенство принимает вид :
Значит,
x∈ (0; 4] ∪[16; + ∞)