1. Алгебра
  2. Найдите минимальное

Найдите минимальное значение функции 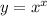y = {x}^{x}
и координаты самой низкой точки. Заранее

Vitas40 Vitas40    2   19.08.2020 00:20    0

Ответы
шпион223709 шпион223709  15.10.2020 16:03

y_{min} = \frac{1}{e} ^\frac{1}{e}

Объяснение:

Здравствуйте!

Преобразуем функцию:

y=x^x = e^{xln(x) }

Найдем наименьшее значение функции:

f(x) =xln(x)

f'(x) = ln(x) +x/x = ln(x)+1 , x\neq 0

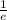ln(x) +1 = 0\\ln(x) = -1\\x=\frac{1}{e}\\\frac{1}{e^2}

То есть \frac{1}{e } - точка минимума.

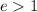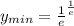
Поскольку e1 , то y_{min} = \frac{1}{e} ^\frac{1}{e}

Если вам понравился ответ, сделай его лучшим.

ПОКАЗАТЬ ОТВЕТЫ
его18 его18  15.10.2020 16:03

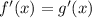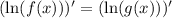По Лопиталю если f'(x) = g'(x), то (\ln(f(x)))' = (\ln(g(x)))'.

Применяем:

y = x^x

\ln(y) = x \cdot \ln(x)

(\ln(y))' = (x \cdot \ln(x))'

\frac{y'(x)}{y(x)} = x' * \ln(x) + x * (\ln(x))'

\frac{y'(x)}{y(x)} = \ln(x) + \frac{x}{x}

\frac{y'(x)}{y(x)} = \ln(x) + 1

y'(x)= y(x) \cdot (\ln(x) + 1)

y'(x)= x^x \cdot (\ln(x) + 1)

Найдем экстремумы:

y'(x)= x^x \cdot (\ln(x) + 1) = 0

Произведение равняется 0, если один из операндов равен 0.

x^x \neq 0, так как 0^0 - неопределённость.

\ln(x) + 1 = 0\\\ln(x) = -1\\x = \frac{1}{e}

y = x^x = (\frac{1}{e})^\frac{1}{e}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
WhiteRout WhiteRout  08.10.2019 21:32
Выполнить , надо. заранее огромное ! ) 1. во вложении 2. зимой аквариумных рыбок кормят 3 раза в неделю. примерная порция на одно кормление: сухая дафния - четверть чайной ложки...
Violet17 Violet17  08.10.2019 21:31
Тест 5. умножение дробей. возведение дроби в степень​...
Mariyana10 Mariyana10  08.10.2019 21:28
Сколько будет 73 целых 66\192 минус 71 целая 136\192? 15 ​...
egorfeklistov egorfeklistov  08.10.2019 21:27
Найти диоганаль прямоугольника и угол, образуемой диагональю и основнанием если высота=8 см, а ширина 3см...
Aalina23 Aalina23  08.10.2019 21:27
F(5)=17найти f(-5) якщо функція являється парною або непарною,, нужно 10 .​...
malygin73rus malygin73rus  15.09.2019 13:10
(2+√x)×(2−√x)+√x найдите производную,...
yadlos38 yadlos38  15.09.2019 13:10
Решите систему уравнений 2x-y=3 |x-2y|=4...
Qqertyi Qqertyi  15.09.2019 13:10
14^6 × 14^-8 14 в 6 степени множить на 14 в минус 8 степени.напишите решения подробно ! 20 б...
маша3025 маша3025  15.09.2019 13:10
За 2,5кг баранины заплатили 475 тенге тогда по той же цене на 665 тенге баранины можно купить...
арманп арманп  10.04.2019 19:31
Подайте число 1 ,2( 3 )у вигляді нескоротного звичайного дробу​...

Популярные вопросы