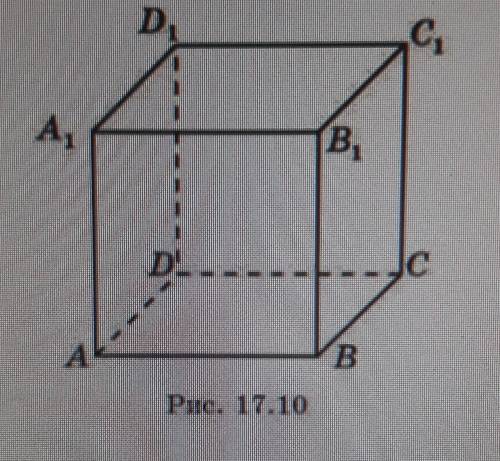
Найдите двухгранные углы , образованные соседними гранями куба (рис. 17. 10):

❗​

Для того чтобы найти двухгранные углы, образованные соседними гранями куба, нужно взглянуть на его рисунок и определить, какие грани считаются соседними.

На рисунке вопроса видно, что куб имеет 6 граней, пронумерованных от 1 до 6. Грани, имеющие общую сторону, являются соседними.

Давайте рассмотрим каждую пару соседних граней и найдем двухгранные углы, образованные ими.

1. Грани 1 и 2: Угол, образованный гранями 1 и 2, будет находиться при пересечении двух плоскостей, соответствующих этим граням. Для того чтобы найти этот угол, нужно найти угол между нормалями к этим плоскостям.

Нормали к грани 1 и грани 2 будут направлены вдоль сторон 1-2-3 и 1-2-4 соответственно. Зная координаты вершин куба, мы можем найти векторы, соединяющие эти вершины и найти их векторное произведение (с использованием правила правой руки для определения знака).

2. Грани 1 и 3: Угол, образованный гранями 1 и 3, будет находиться при пересечении двух плоскостей, соответствующих этим граням. Для того чтобы найти этот угол, нужно найти угол между нормалями к этим плоскостям.

Нормали к грани 1 и грани 3 будут направлены вдоль сторон 1-2-3 и 1-3-5 соответственно. Зная координаты вершин куба, мы можем найти векторы, соединяющие эти вершины и найти их векторное произведение (с использованием правила правой руки для определения знака).

3. Грани 1 и 4: Угол, образованный гранями 1 и 4, будет находиться при пересечении двух плоскостей, соответствующих этим граням. Для того чтобы найти этот угол, нужно найти угол между нормалями к этим плоскостям.

Нормали к грани 1 и грани 4 будут направлены вдоль сторон 1-2-4 и 1-4-6 соответственно. Зная координаты вершин куба, мы можем найти векторы, соединяющие эти вершины и найти их векторное произведение (с использованием правила правой руки для определения знака).

4. Грани 1 и 5: Угол, образованный гранями 1 и 5, будет находиться при пересечении двух плоскостей, соответствующих этим граням. Для того чтобы найти этот угол, нужно найти угол между нормалями к этим плоскостям.

Нормали к грани 1 и грани 5 будут направлены вдоль сторон 1-3-5 и 1-4-5 соответственно. Зная координаты вершин куба, мы можем найти векторы, соединяющие эти вершины и найти их векторное произведение (с использованием правила правой руки для определения знака).

5. Грани 1 и 6: Угол, образованный гранями 1 и 6, будет находиться при пересечении двух плоскостей, соответствующих этим граням. Для того чтобы найти этот угол, нужно найти угол между нормалями к этим плоскостям.

Нормали к грани 1 и грани 6 будут направлены вдоль сторон 1-3-6 и 1-4-6 соответственно. Зная координаты вершин куба, мы можем найти векторы, соединяющие эти вершины и найти их векторное произведение (с использованием правила правой руки для определения знака).

Таким образом, для каждой пары соседних граней куба, мы можем найти двухгранный угол используя векторные операции.